ما هو سيناريو الحياة الواقعية الذي يتضمن معادلات من الدرجة الثانية?
هناك الكثير من المواقف الحقيقية التي تنطوي على التربيعات والقطوع المكافئة. رمي الكرة, اطلاق النار على مدفع, الغوص خارج المنصة, وضرب كرة الجولف كلها أمثلة على المواقف التي يمكن محاكاتها باستخدام وظائف تربيعية.
تُستخدم المعادلة التربيعية عمليًا في علم الفلك, الرياضيات, هندسة, دواء, المالية, الحراجة, العلم أو البحث, إلخ. في اي مجال, إذا كان هناك نشاط أكاديمي أو بحثي, من المحتمل أن يكون هناك نظام معادلات قد يتطلب حل معادلة تربيعية.
للحياة العادية, دون استخدام أي مواد أكاديمية, ليست هناك حاجة إلى الرياضيات أو المعادلات; و, وبالتالي, المعادلة التربيعية غير مطلوبة.
ستندهش من عدد التطبيقات التي تستخدم المعادلات التربيعية.
ارمي الكرة في الهواء. القوس الذي يتبعه هو قطع مكافئ. ويمكن تمثيل القطع المكافئ بمعادلة تربيعية.
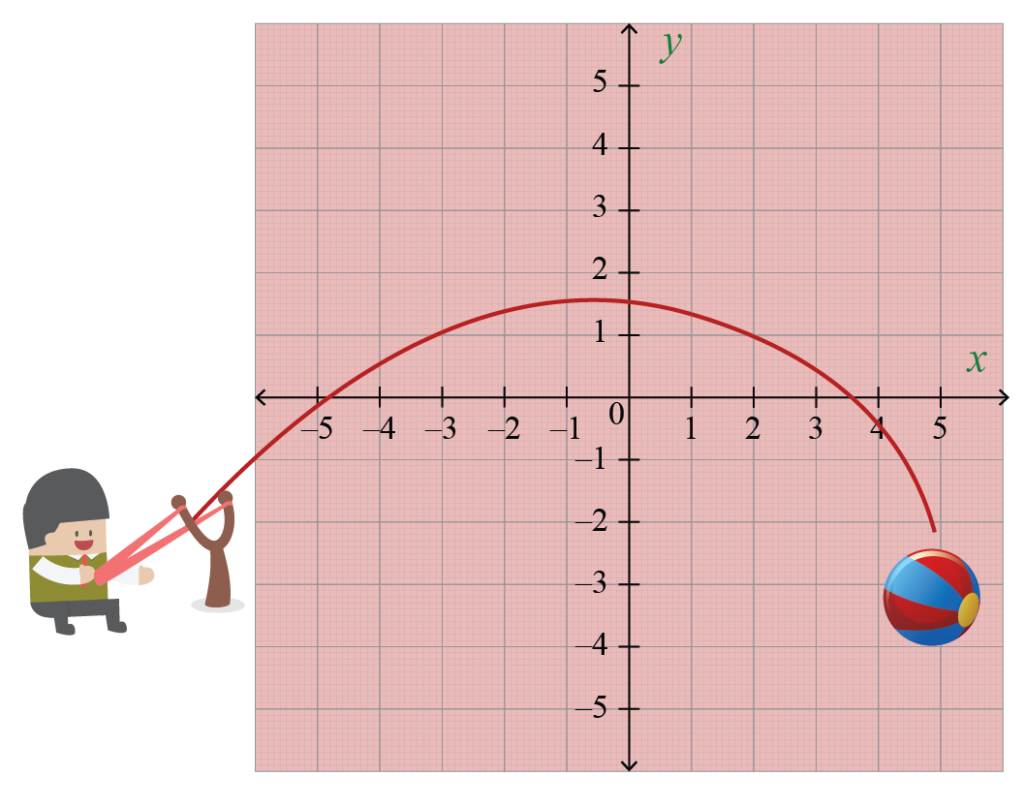
ما هو تركيز القطع المكافئ? تتمثل إحدى طرق تعريف القطع المكافئ في أنها مجموعة النقاط الموجودة في المستوى على مسافة متساوية من خط معين, يسمى الدليل, ونقطة معينة, يسمى التركيز.
كيف يتم تطبيق المعادلات التربيعية في حياتنا اليومية?
غالبًا ما تستخدم المعادلات التربيعية في الحياة اليومية. تتناسب قوة الجاذبية طرديًا مع المربع العكسي للمسافة من الأرض, حتى المقذوفات, من كرة تنس إلى صاروخ, تطير على طول مسار مكافئ.
افترض أنك تريد تحريك القهوة, قوة الجاذبية المركزية للقهوة تربيعية في الطبيعة, لذلك عند إزالة الملعقة, تدرك أنه يشكل شكلًا مكافئًا (تخيل قطع مكافئ ثلاثي الأبعاد).
غالبًا ما تُستخدم المعادلات التربيعية في مشاكل التحسين في كل من الهندسة والتمويل, عندما تريد تقليل تكلفة سلعة معينة أو زيادة الربح إلى الحد الأقصى, وأحيانًا يمكن نمذجة ذلك بواسطة المعادلات التربيعية (وإن لم يكن دائمًا).
تتطلب طريقة تحديد مقاومة المقاومات بالتوازي فهمًا عمليًا لحل المعادلات التربيعية, إذا كنت تعرف بعض الاستنتاجات, لذلك من المهم أن يكون لديك التركيبة الصحيحة من المقاومات حتى لا تدمر عناصر الدائرة المهمة.
تستخدم المرايا والميكروفونات ذات القطع المكافئ نفس ميزة القطع المكافئ وبالتالي نظائرها المكافئة, وهو أنه يمكنهم تركيز الانعكاسات عند نقطة واحدة, مما يعطي صورة جيدة جدًا للتلسكوب أو إشارة واضحة من الميكروفون.
الآن لا تزال بعض التطبيقات اليومية, ولكن على نطاق أوسع, هي في ODEs من الدرجة الثانية, التي تتطلب معادلة مساعدة لحلها, وهي معادلة من الدرجة الثانية, والتي تحدد نتيجتها وظيفة النظام بأكمله.
أمثلة على استخدامات هذه المعادلة هي التأرجحات التي تستخدم الحركة التوافقية البسيطة, مثل النوابض في سيارتك أو الزنبركات الموجودة في معظم الأجهزة الميكانيكية على الأرض.
أصل المعادلة التربيعية
كان البابليون أول من اخترع المعادلات التربيعية منذ عام 2000 قبل الميلاد. لقد احتاجوا إليها من أجل حسابات الزراعة والري.
استخدمها الإغريق لاحقًا – لجأ أرخميدس إليهم لإيجاد قيمة نصف قطر الدائرة.
اليوم نستخدمها كل يوم لحساب المساحة (حجم الصندوق, غرفة معيشة, قطعة أرض), لتحديد ربح سلعة ما (كم أحتاج من هذه السلعة لبيعها لتحقيق ربح?) أو لتقدير سرعة الجسم (إذا رميت شيئًا عليك – شيء صلب, – كم من الوقت سيستغرق الأمر حتى ينتهي بي الأمر بين يديك?)
أسباب الرغبة في إيجاد حل لمثل هذه المشاكل غير معروفة بالكامل, لكن يمكننا أن نجعل التخمينات.
فمثلا, قد يكون لديهم كمية معينة من المواد لإحاطة حقل مستطيل لمنطقة معينة. ربما كانوا بحاجة إلى معرفة الكمية المثالية من المواد لاستخدامها لهذا المحيط, أو إذا كان لديهم ما يكفي.
مهما كانت احتياجاتهم, لديهم حل للمشكلة. قاموا بتدوينها خطوة بخطوة على النحو التالي:
س + و =الصورة; ………………………………………… (1)
س ص=ا; ……………………………………………. (2)
(1) أوجد نصف الصورة.
(2) قم بتربيع الرقم الذي تم الحصول عليه في 1.
(3) اطرح الرقم الموجود في 2 بواسطة ا.
(4) أوجد الجذر التربيعي للرقم الموجود فيه 3.
(5) أضف الرقم الذي تم الحصول عليه في 1 للرقم الذي تم الحصول عليه في 4 ، هذا هو طول أحد الأضلاع.
أداء الخطوة 4 كان الجزء الأصعب, على الرغم من أن البابليين معروفون باستخدامهم الجداول المربعة, من المفترض أنها تحتوي على قائمة بأرقام مربعة, لتقريب الجذر التربيعي لرقم.
ينسب بعض المؤرخين أيضًا إلى البابليين أول تطبيق لطريقة نيوتن, والذي تم استخدامه تحديدًا لإيجاد الجذور التربيعية.
الشيء المثير للاهتمام في كل هذا هو كيفية استخدام الصيغة التربيعية (∗) نشأت من مثل هذه المشكلة. بعد كل شيء, نحن لا نحل معادلة من الدرجة الثانية هنا, لكن زوج من المعادلات الآنية (1) و (2).
هذا ليس من الصعب رؤيته, باستخدام تدوينات اليوم. من عند (1) نحصل على y = s-x, والتي عند استبدالها في (2) يعطي:
س(الصورة-س)=ا.
الصورةس-س2=ا.
س2-الصورةس+ا=0.
وهكذا, (1) و (2) تعادل حل المعادلة التربيعية x2-sx + أ = 0. على وجه التحديد, هذا يخبرنا أنه في هذه المعادلة التربيعية, معامل x هو سالب مجموع الحلين (معادلة (1) ), ومعامل واحد هو حاصل ضرب الحلين (معادلة (2) ).



أضف إجابة
يجب عليك تسجيل الدخول او التسجيل لتستطيع اضافه إجابة .