Was ist mechanische Energie? Ich brauche eine umfassende Definition
Was ist mechanische Energie
 in der Physik, mechanische Energie (Emech) ist die Energie, die mit dem verbunden ist Bewegung und Position eines Objekts normalerweise in einem Kraftfeld (z.B.. Schwerkraftfeld). Mechanische Energie (und auch die thermische Energie) kann in zwei Kategorien unterteilt werden, vorübergehend und gespeichert. Transiente Energie ist Energie in Bewegung, das ist, Energie, die von einem Ort zum anderen übertragen wird. Gespeicherte Energie ist die Energie, die in einer Substanz oder einem Objekt enthalten ist. Transiente mechanische Energie wird allgemein als bezeichnet Arbeit. Gespeicherte mechanische Energie existiert in einer von zwei Formen: kinetisch oder Potenzial:
in der Physik, mechanische Energie (Emech) ist die Energie, die mit dem verbunden ist Bewegung und Position eines Objekts normalerweise in einem Kraftfeld (z.B.. Schwerkraftfeld). Mechanische Energie (und auch die thermische Energie) kann in zwei Kategorien unterteilt werden, vorübergehend und gespeichert. Transiente Energie ist Energie in Bewegung, das ist, Energie, die von einem Ort zum anderen übertragen wird. Gespeicherte Energie ist die Energie, die in einer Substanz oder einem Objekt enthalten ist. Transiente mechanische Energie wird allgemein als bezeichnet Arbeit. Gespeicherte mechanische Energie existiert in einer von zwei Formen: kinetisch oder Potenzial:
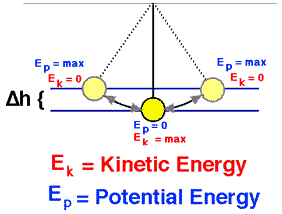
- Potenzielle Energie. Potenzielle Energie, die, ist definiert als die Energie, die in einem Objekt gespeichert ist, das einer konservativen Kraft ausgesetzt ist. Übliche Typen umfassen die potenzielle Gravitationsenergie eines Objekts, die von seiner Masse und seinem Abstand vom Massenmittelpunkt eines anderen Objekts abhängt.
- Kinetische Energie. Die kinetische Energie, K, ist definiert als die Energie, die in einem Objekt aufgrund seiner Bewegung gespeichert ist. Es hängt von der Geschwindigkeit eines Objekts ab und ist die Fähigkeit eines sich bewegenden Objekts, an anderen Objekten zu arbeiten, wenn es mit ihnen kollidiert.
Erhaltung der mechanischen Energie
Zuerst das Prinzip der Erhaltung der mechanischen Energie wurde angegeben:
Die gesamte mechanische Energie (definiert als die Summe seiner potentiellen und kinetischen Energie) auf ein Teilchen wirken nur konservative Kräfte ist konstant.
Siehe auch: Erhaltung der mechanischen Energie
Ein isoliertes System ist einer, in dem keine äußere Kraft verursacht Energieveränderungen. Wenn nur konservative Kräfte auf ein Objekt einwirken und die ist der potenzielle Energie Funktion für die konservative Gesamtkraft, dann
Emech = u + K
Die potentielle Energie, die, hängt von der Position eines Objekts ab, das einer konservativen Kraft ausgesetzt ist.
Sie ist definiert als die Fähigkeit des Objekts, Arbeit zu verrichten, und wird erhöht, wenn das Objekt in die entgegengesetzte Richtung der Kraftrichtung bewegt wird.
Die potentielle Energie einem System zugeordnet ist, das aus der Erde und einem nahegelegenen Teilchen besteht potentielle Energie der Gravitation.
Die kinetische Energie, K, hängt von der Geschwindigkeit eines Objekts ab und ist die Fähigkeit eines sich bewegenden Objekts, an anderen Objekten zu arbeiten, wenn es mit ihnen kollidiert.
K = ½ mv2
Die oben genannte Definition (Emech = u + K) geht davon aus, dass das System ist frei von Reibung und andere nichtkonservative Kräfte. Der Unterschied zwischen einer konservativen und einer nicht-konservativen Kraft besteht darin, dass eine konservative Kraft ein Objekt von einem Punkt zum anderen bewegt, die von der konservativen Kraft verrichtete Arbeit ist unabhängig vom Weg.
In jeder realen Situation, Reibungskräfte und andere nichtkonservative Kräfte sind vorhanden, aber in vielen Fällen sind ihre Auswirkungen auf das System so gering, dass das Prinzip der Erhaltung der mechanischen Energie kann als gute Annäherung verwendet werden. Beispielsweise ist die Reibungskraft eine nicht konservative Kraft, weil es wirkt, um die mechanische Energie in einem System zu reduzieren.
Beachten Sie, dass nicht konservative Kräfte die mechanische Energie nicht immer reduzieren. Eine nichtkonservative Kraft ändert die mechanische Energie, Es gibt Kräfte, die die gesamte mechanische Energie erhöhen, wie die Kraft, die von einem Motor oder Motor bereitgestellt wird, ist auch eine nichtkonservative Kraft.
Blockieren Sie das Herunterrutschen einer reibungslosen Steigung
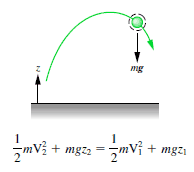
Das 1 kg-Block beginnt mit einer Höhe H (nehmen wir mal an 1 m) über dem Boden, mit potenzielle Energie mgH und kinetische Energie das ist gleich 0. Es rutscht zu Boden (ohne Reibung) und kommt ohne potentielle Energie und kinetische Energie an K = ½ mv2. Berechnen Sie die Geschwindigkeit des Blocks auf dem Boden und seine kinetische Energie.
Emech = u + K = konst
=> ½ Mw2 = mgH
=> v = √2gH = 4.43 Frau
=> K2 = ½ x 1 kg x (4.43 Frau)2 = 19.62 kg.m2.s-2 = 19.62 J.
Pendel
 Angenommen a Pendel (Kugel der Masse m, die an einer langen Schnur aufgehängt ist L dass wir hochgezogen haben, damit der Ball eine Höhe hat H < L über seinem tiefsten Punkt auf dem Bogen seiner gestreckten Saitenbewegung. Das Pendel wird dem ausgesetzt konservative Gravitationskraft wo Reibungskräfte wie Luftwiderstand und Reibung am Drehpunkt vernachlässigbar sind.
Angenommen a Pendel (Kugel der Masse m, die an einer langen Schnur aufgehängt ist L dass wir hochgezogen haben, damit der Ball eine Höhe hat H < L über seinem tiefsten Punkt auf dem Bogen seiner gestreckten Saitenbewegung. Das Pendel wird dem ausgesetzt konservative Gravitationskraft wo Reibungskräfte wie Luftwiderstand und Reibung am Drehpunkt vernachlässigbar sind.
Wir befreien es von der Ruhe. Wie schnell geht es unten?
Das Pendel reicht größte kinetische Energie und geringste potentielle Energie wenn im vertikale Position, weil es an diesem Punkt die größte Geschwindigkeit haben und der Erde am nächsten sein wird. Auf der anderen Seite, es wird seine haben geringste kinetische Energie und größte potentielle Energie Beverly Hills Extrempositionen seines Schwungs, weil es an diesen Punkten die Geschwindigkeit Null hat und am weitesten von der Erde entfernt ist.
Wenn die Amplitude auf kleine Ausschläge beschränkt ist, die Periode T eines einfachen Pendels, die Zeit, die für einen vollständigen Zyklus benötigt wird, ist:
woher L ist die Länge des Pendels und G ist die lokale Erdbeschleunigung. Bei kleinen Schaukeln ist die Schaukeldauer für Schaukeln unterschiedlicher Größe ungefähr gleich. Das ist, die Periode ist amplitudenunabhängig.



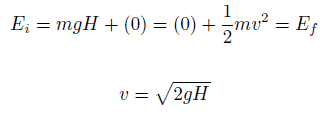
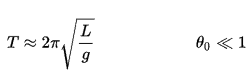
Lassen Sie eine Antwort
Sie müssen Anmeldung oder registrieren um eine neue Antwort hinzuzufügen.