Estas tre simple identigi la x kaj y-interkaptojn sur grafeo, sed studentoj ofte luktas por trovi ilin uzante nur la ekvacion. Tamen, ĝi nur postulas simplan lertaĵon:

Por trovi la x-interkapton(s) de ekvacio, anstataŭaĵo en y = 0 kaj solvu por x.

Por trovi la y-interkapton(s) de ekvacio, anstataŭigu en x = 0 kaj solvu por y.

La X-Interkaptoj

La x-interkaptoj estas punktoj kie la grafikaĵo de funkcio aŭ ekvacio krucas aŭ "tuŝas" la x-akson de la Kartezia Ebeno. Vi povas pensi pri tio kiel punkto kun y-valoro de nulo.

• Trovi la x-interkaptojn de ekvacio, lasu $Y=0$ tiam solvu por $x$.
• En punktonotacio, ĝi estas skribita kiel \foriris( {x,0} \ĝuste)(x,0).

x-interkapto de Lineara Funkcio aŭ a Rekte Linio

x-interkaptoj de Kvadratiko Funkcio aŭ Parabolo

La Y-Interkaptoj

La y-interkaptoj estas punktoj kie la grafikaĵo de funkcio aŭ ekvacio krucas aŭ "tuŝas" la y-akson de la Kartezia Ebeno. Vi povas pensi pri tio kiel punkto kun x-valoro de nulo.

• Trovi la y-interkaptojn de ekvacio, lasu $x=0$ tiam solvu por $Y$.
• En punktonotacio, ĝi estas skribita kiel \foriris( {0,Y} \ĝuste)(0,Y).

y-interkapto de Linia Funkcio aŭ Rekta Linio

y-interkapto de Kvadratika Funkcio aŭ Parabolo

Ekzemploj de Kiel Trovi la x kaj y-interkaptojn de Linio, Parabolo, kaj Rondo

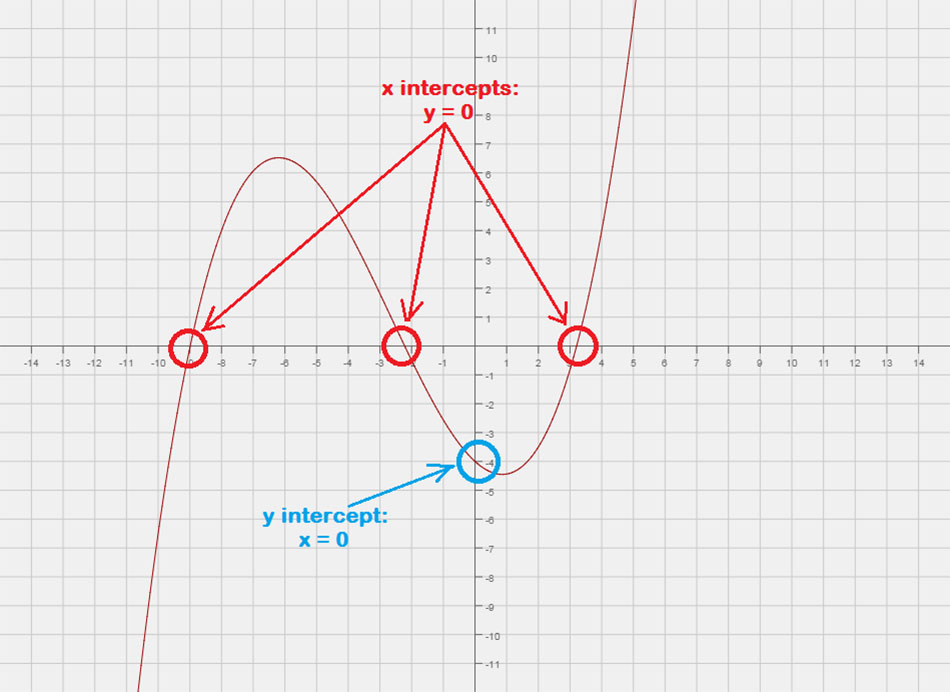
Ekzemplo 1: El la grafikaĵo, priskribu la x kaj y-interkaptojn uzante punktonotacion.

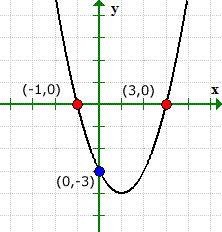
La grafeo krucas la x-akson je x = 1 kaj x = 3, tial, ni povas skribi la x-interkaptojn kiel punktojn (1,0) kaj (–3, 0).

simile, la grafeo krucas la y-akson je Y = 3. Ĝia y-interkapo povas esti skribita kiel la punkto (0,3).

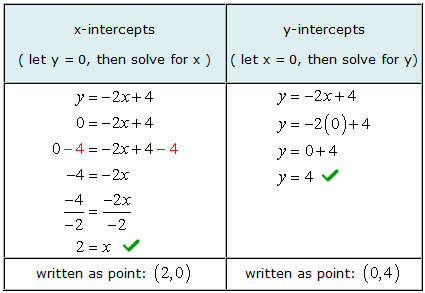
Ekzemplo 2: Trovu la x kaj y-interkaptojn de la linio Y = –2x + 4.

Trovi la x-interkaptojn algebre, ni lasas Y = 0 en la ekvacio kaj poste solvu por valoroj de x. En la sama maniero, trovi por y-interkaptoj algebre, ni lasas x = 0 en la ekvacio kaj poste solvu por Y.

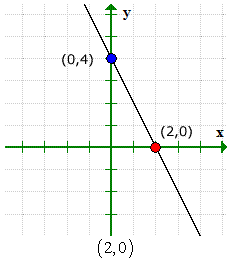
Jen la grafikaĵo por kontroli, ke niaj respondoj estas ĝustaj.

Ekzemplo 3: Trovu la x kaj y-interkaptojn de la kvadrata ekvacio Y = x² − 2x − 3.

La grafikaĵo de ĉi tiu kvadrata ekvacio estas parabolo. Ni atendas ke ĝi havu "U" formon kie ĝi aŭ malfermus supren aŭ malsupren.

Solvi por la x-interkapto de ĉi tiu problemo, vi faros faktoro simpla trinomo. Tiam vi starigas ĉiun dunomfaktoron egala al nulo kaj solvu por x.

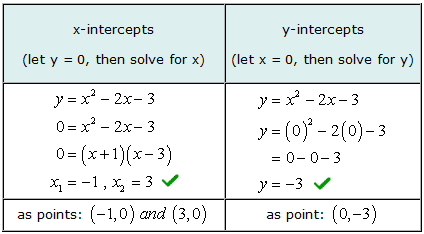
Niaj solvitaj valoroj por kaj x kaj y-interkaptoj kongruas kun la grafika solvo.

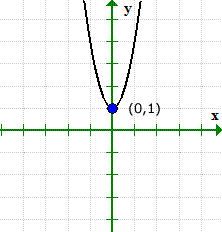
Ekzemplo 4: Trovu la x kaj y-interkaptojn de la kvadrata ekvacio Y = 3x² + 1.

Ĉi tio estas ekzemplo kie la grafeo de la ekvacio havas y-interkapton sed sen x-interkapo.

• Ni unue trovu la y-interkapton ĉar ĝi estas ege facila! Enŝaltu x = 0 tiam solvu por y.

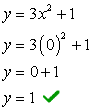
• Nun por la x-interkapto. Enŝaltu y = 0, kaj solvu por x.

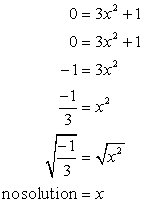
La kvadrata radiko de negativa nombro estas imaga. Ĉi tio sugestas ke ĉi tiu ekvacio ne havas x-interkapto!

La grafikaĵo povas kontroli kio okazas. Rimarku ke la grafeo transiris la y-akson je (0,1), sed neniam faris kun la x-akso.

Ekzemplo 5: Trovu la x kaj y-interkaptojn de la cirklo (x + 4)² + (Y + 2)² = 8.

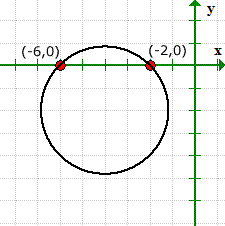
Ĉi tio estas bona ekzemplo por ilustri ke estas eble ke la grafikaĵo de ekvacio havu x-interkaptojn sed sen y-interkaptojn..

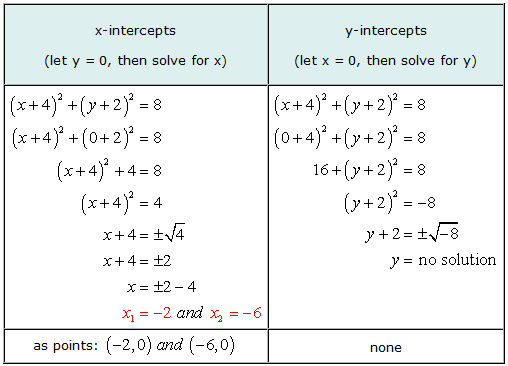
Solvante por y, ni alvenis al la situacio provi akiri la kvadratan radikon de negativa nombro. La respondo estas imaga, tiel, neniu solvo. Tio signifas, ke la ekvacio ne havas iujn ajn y-interkaptojn.

La grafeo kontrolas ke ni pravas por la valoroj de niaj x-interkaptoj, kaj ĝi ne havas y-interkaptojn.

Kredito:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/