Kio Estas La Reala Viva Scenaro Engaĝanta Kvadratajn Ekvaciojn?
Estas multaj realaj situacioj implikantaj kvadratojn kaj parabolojn. Ĵetante pilkon, pafante kanonon, plonĝado de platformo, kaj trafi golfpilkon estas ĉiuj ekzemploj de situacioj kiuj povas esti simulitaj uzante kvadratajn funkciojn.
La kvadrata ekvacio estas praktike uzata en astronomio, matematiko, studentoj estas enskribitaj en majstraj kaj doktoraj programoj trans, medikamento, financo, forstado, scienco aŭ esploro, ktp. En ajna kampo, se estas akademia aŭ esplora agado, verŝajne ekzistas sistemo de ekvacioj kiuj povas postuli kvadratan ekvacion por solvi.
Por ordinara vivo, sen la uzo de iuj akademiaj materialoj, matematiko aŭ ekvacioj ne estas bezonataj; kaj, tial, kvadrata ekvacio ne estas postulata.
Vi estos surprizita de la nombro da aplikoj, kiuj uzas kvadratajn ekvaciojn.
Ĵetu pilkon en la aeron. La arko, kiun ĝi sekvas, estas parabolo. Kaj parabolo povas esti reprezentita per kvadrata ekvacio.
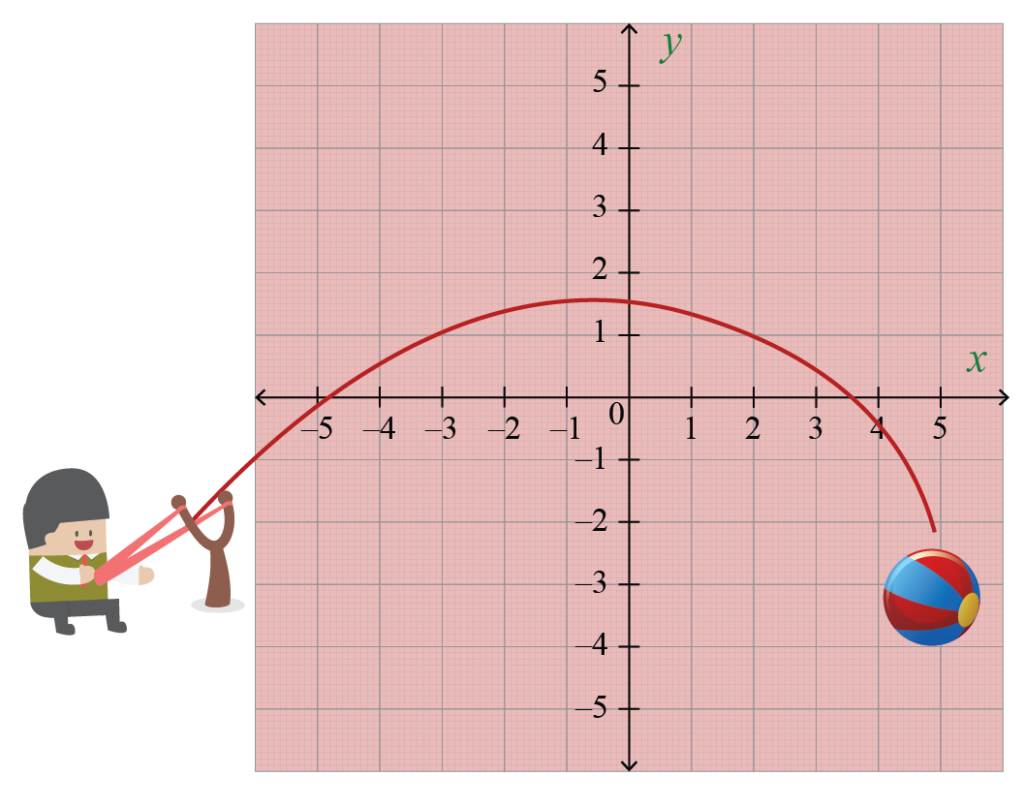
Kio estas la fokuso de parabolo? Unu maniero difini parabolon estas ke ĝi estas la aro de punktoj en la ebeno egaldistanca de antaŭfiksita linio, nomita la direktisto, kaj donita punkto, nomita la fokuso.
Kiel estas aplikataj kvadrataj ekvacioj en nia ĉiutaga vivo?
Kvadrataj ekvacioj estas ofte uzataj en ĉiutaga vivo. La forto de gravito estas proporcia al la inversa kvadrato de la distanco de la Tero, do ĵetaĵoj, de tenisa pilko al raketo, flugi laŭ parabola trajektorio.
Supozu, ke vi volas movi kafon, la centripeta forto de kafo estas kvadrata en naturo, do kiam vi forigas la kuleron, vi rimarkas, ke ĝi formas paraboloidan formon (imagu tridimensian parabolon).
Kvadrataj ekvacioj ofte estas uzitaj en optimumproblemoj en kaj inĝenieristiko kaj financo, kiam vi volas minimumigi la koston de aparta bono aŭ maksimumigi profiton, kaj foje ĉi tio povas esti modeligita per kvadrataj ekvacioj (kvankam ne ĉiam).
La maniero determini la reziston de la rezistiloj paralele postulas laborkomprenon de solvado de kvadrataj ekvacioj, se vi konas kelkajn konkludojn, do gravas havi la ĝustan kombinaĵon de rezistiloj por ne detrui gravajn cirkvitajn elementojn.
Parabolaj speguloj kaj mikrofonoj uzas la saman trajton de paraboloj kaj tial paraboloidoj, kiu estas ke ili povas koncentri reflektojn ĉe unu punkto, kiu donas tre bonan bildon por teleskopo aŭ klaran signalon de mikrofono.
Nun kelkaj ankoraŭ ĉiutagaj aplikoj, sed sur pli granda skalo, estas en 2-a ordo ODE-oj, kiuj postulas helpan ekvacion por solvi, kiu estas kvadrata ekvacio, kaj kies rezulto determinas la funkcion por la tuta sistemo.
Ekzemploj de uzoj de ĉi tiu ekvacio estas svingoj kiuj uzas simplan harmonian movon, kiel la risortoj en via aŭto aŭ la risortoj en la plej multaj mekanikaj aparatoj surgrunde.
Origino De Kvadrata Ekvacio
La babilonanoj estis la unuaj se temas pri inventi kvadratajn ekvaciojn jam en 2000 a.K. Ili bezonis ilin por agrikulturaj kaj irigaciaj kalkuloj.
La grekoj uzis ilin poste – Arkimedo frekventis ilin por trovi la valoron de la radiuso de cirklo.
Hodiaŭ ni uzas ilin ĉiutage por kalkuli areon (la grandeco de skatolo, salono, terpeco), por determini la profiton de varo (kiom da ĉi tiu varo mi bezonas vendi por fari profiton?) aŭ taksi la rapidecon de objekto (se mi ion ĵetos al vi – io solida, – kiom da tempo daŭros, ke tio, kion mi ĵetas, finiĝos en viajn manojn?)
La kialoj de voli trovi solvon al tiaj problemoj ne estas plene konataj, sed ni povas fari divenojn.
Ekzemple, ili eble havis certan kvanton da materialo kun kiu enfermi rektangulan kampon de antaŭfiksita areo. Eble ili bezonis scii, kia estas la ideala kvanto da materialo por uzi por tiu perimetro, aŭ se ili havus sufiĉe.
Kiaj ajn iliaj bezonoj, ili ja havis solvon al la problemo. Ili skribis ĝin paŝon post paŝo jene:
x + Y =s; ………………………………………… (1)
xy=a; ……………………………………………. (2)
(1) Trovu duonon de s.
(2) Kvadratigu la nombron akiritan en 1.
(3) Subtrahi la nombron trovitan en 2 de a.
(4) Trovu la kvadratan radikon de la nombro trovita en 3.
(5) Aldonu la nombron akiritan en 1 al la nombro akirita en 4.Tio estas la longo de unu el la flankoj.
Farante paŝon 4 estis la plej malfacila parto, kvankam oni scias, ke la babilonanoj uzis kvadratajn tablojn, supozeble enhavanta liston de kvadrataj nombroj, por proksimigi la kvadratan radikon de nombro.
Kelkaj historiistoj ankaŭ atribuas al la babilonanoj la plej unuan aplikon de la metodo de Neŭtono, kiu estis uzata specife por trovi kvadratajn radikojn.
Lin interesa pri ĉio ĉi estas kiel la kvadrata formulo (∗) estiĝis el tia problemo. Finfine, ni ne solvas kvadratan ekvacion ĉi tie, sed paro da samtempaj ekvacioj (1) kaj (2).
Ĉi tio ne estas malfacile vidi, uzante la hodiaŭajn notaciojn. De (1) ni ricevas y=s-x, kiun kiam anstataŭigite en (2) donas:
x(s−x)=a.
sx−x2=a.
x2−sx+a=0.
Tiel, (1) kaj (2) estas ekvivalentaj al solvado de la kvadrata ekvacio x2-sx+a=0. Specife, ĉi tio diras al ni, ke en ĉi tiu kvadrata ekvacio, la koeficiento de x estas la negativo de la sumo de la du solvoj (ekvacio (1) ), kaj la koeficiento de unu estas la produkto de la du solvoj (ekvacio (2) ).



Lasu respondon
Vi devas Ensaluti aŭ registri aldoni novan respondon.