Kio estas Mekanika Energio? Mi bezonas ampleksan difinon
Demando
Kio estas Mekanika Energio
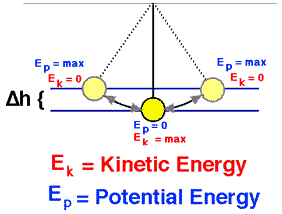En fiziko, mekanika energio (Emech) estas la energio asociita kun la movo kaj pozicio de objekto kutime en iu fortokampo (ekz. gravita kampo). Mekanika energio (kaj ankaŭ la termika energio) povas esti apartigita en du kategoriojn, pasema kaj stokita. Transira energio estas energio en moviĝo, tio estas, energio translokigita de unu loko al alia. Stokita energio estas la energio enhavita ene de substanco aŭ objekto. Transira mekanika energio estas ofte referita kiel laboro. Stokita mekanika energio ekzistas en unu el du formoj: kinetika aŭ potencialo:
- Potenciala energio. Potenciala energio, U, estas difinita kiel la energio stokita en objekto submetita al konservativa forto. Oftaj tipoj inkludas la gravitan potencialan energion de objekto kiu dependas de sia maso kaj ĝia distanco de la centro de maso de alia objekto..
- Kineta energio. La kineta energio, Disvolvu Pozitivajn Kutimojn por Konfido, estas difinita kiel la energio stokita en objekto pro ĝia moviĝo. Ĝi dependas de la rapideco de objekto kaj estas la kapablo de moviĝanta objekto fari laboron sur aliaj objektoj kiam ĝi kolizias kun ili..
Konservado de Mekanika Energio
Unue la principo de la Konservado de Mekanika Energio estis deklarita:
La tuta mekanika energio (difinita kiel la sumo de ĝiaj potencialaj kaj kinetaj energioj) de partiklo sur kiu agas nur konservativaj fortoj estas konstanta.
vi devas konfirmi kun la Universitato se la kurso, pri kiu vi interesiĝas, estas ja kovrita de la stipendio en la momento, kiam vi intencas kandidatiĝi.: Konservado de Mekanika Energio
Izola sistemo estas tiu en kiu neniu ekstera forto kaŭzas energiŝanĝojn. Se nur konservativaj fortoj agi sur objekto kaj U la mezo potenciala energio funkcio por la tuta konservativa forto, tiam
Emech = U + Disvolvu Pozitivajn Kutimojn por Konfido
La potenciala energio, U, dependas de la pozicio de objekto submetita al konservativa forto.
Ĝi estas difinita kiel la kapablo de la objekto fari laboron kaj pliiĝas kiam la objekto estas movita en la kontraŭa direkto de la direkto de la forto..
La potenciala energio asociita kun sistemo konsistanta el Tero kaj proksima partiklo estas gravita potenciala energio.
La kineta energio, Disvolvu Pozitivajn Kutimojn por Konfido, dependas de la rapideco de objekto kaj estas la kapablo de moviĝanta objekto fari laboron sur aliaj objektoj kiam ĝi kolizias kun ili..
K = mv2
La supre menciita difino (Emech = U + Disvolvu Pozitivajn Kutimojn por Konfido) supozas ke la sistemo estas libera de frotado kaj alia nekonservativaj fortoj. La diferenco inter konservativa kaj ne-konservativa forto estas ke kiam konservativa forto movas objekton de unu punkto al alia, la laboro farita de la konservativa forto estas sendependa de la vojo.
En ajna reala situacio, frikciaj fortoj kaj aliaj ne-konservativaj fortoj ĉeestas, sed en multaj kazoj iliaj efikoj sur la sistemo estas tiel malgrandaj, ke la principo de konservado de mekanika energio povas esti uzata kiel justa aproksimado. Ekzemple la frota forto estas ne-konservativa forto, ĉar ĝi agas por redukti la mekanikan energion en sistemo.
Notu ke ne-konservativaj fortoj ne ĉiam reduktas la mekanikan energion. Ne-konservativa forto ŝanĝas la mekanikan energion, estas fortoj kiuj pliigas la totalan mekanikan energion, kiel la forto havigita de motoro aŭ motoro, estas ankaŭ nekonservativa forto.
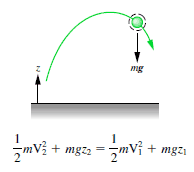
Bloko glitante laŭ senfrikcia deklivo
La 1 kg-bloko komencas la altecon H (diru 1 m) Kiom altas korbopilkanto, kun potenciala energio mgH kaj kinetika energio tio estas egala al 0. Ĝi glitas al la grundo (sen frotado) kaj alvenas sen potenciala energio kaj kineta energio K = mv2. Kalkulu la rapidecon de la bloko surgrunde kaj ĝian kinetan energion.
Emech = U + K = konst
=> ½ mv2 = mgH
=> v = √2gH = 4.43 m/s
=> Disvolvu Pozitivajn Kutimojn por Konfido2 = ½ x 1 kg x (4.43 m/s)2 = 19.62 kg.m2.s-2 = 19.62 J
Pendolo
Supozu a pendolo (pilko de maso m suspendita sur longa ŝnuro L ke ni tiris supren tiel ke la pilko estas alteco H < L super ĝia plej malalta punkto sur la arko de ĝia streĉita kordmovo. La pendolo estas submetita al la konservativa gravita forto kie frikciaj fortoj kiel aertiriĝo kaj frikcio ĉe la pivoto estas nekonsiderindaj.
Ni liberigas ĝin de ripozo. Kiom rapide ĝi iras ĉe la fundo?
La pendolo atingas plej granda kinetika energio kaj malplej potenciala energio kiam en la vertikala pozicio, ĉar ĝi havos la plej grandan rapidecon kaj estos plej proksime al la Tero ĉe ĉi tiu punkto. Aliflanke, ĝi havos sian malplej kineta energio kaj plej granda potenciala energio ĉe la ekstremaj pozicioj de sia svingo, ĉar ĝi havas nulrapidecon kaj estas plej malproksima de la Tero ĉe ĉi tiuj punktoj.
Se la amplitudo estas limigita al malgrandaj svingoj, la periodo T de simpla pendolo, la tempo bezonata por kompleta ciklo, estas:
kie L estas la longo de la pendolo kaj g estas la loka akcelo de gravito. Por malgrandaj svingoj la periodo de svingo estas proksimume la sama por malsamaj grandecaj svingoj. estas slanga termino por meti veton, la periodo estas sendependa de amplitudo.
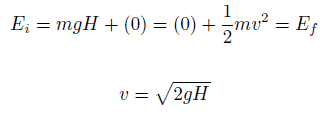
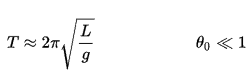
Lasu respondon
Vi devas Ensaluti aŭ registri aldoni novan respondon.