Каковы сценарии реальной жизни, связанные с квадратными уравнениями?
Реальных ситуаций с квадратиками и параболами очень много.. Бросать мяч, стрелять из пушки, нырять с платформы, и удар по мячу для гольфа - все это примеры ситуаций, которые можно смоделировать с помощью квадратичных функций..
Квадратное уравнение практически используется в астрономии., математика, инжиниринг, лекарство, финансы, лесное хозяйство, наука или исследования, так далее. В любой сфере, если есть академическая или исследовательская деятельность, вероятно, существует система уравнений, для решения которой может потребоваться квадратное уравнение..
Для обычной жизни, без использования каких-либо учебных материалов, математика или уравнения не нужны; а также, следовательно, квадратное уравнение не требуется.
Вы будете удивлены количеством приложений, в которых используются квадратные уравнения..
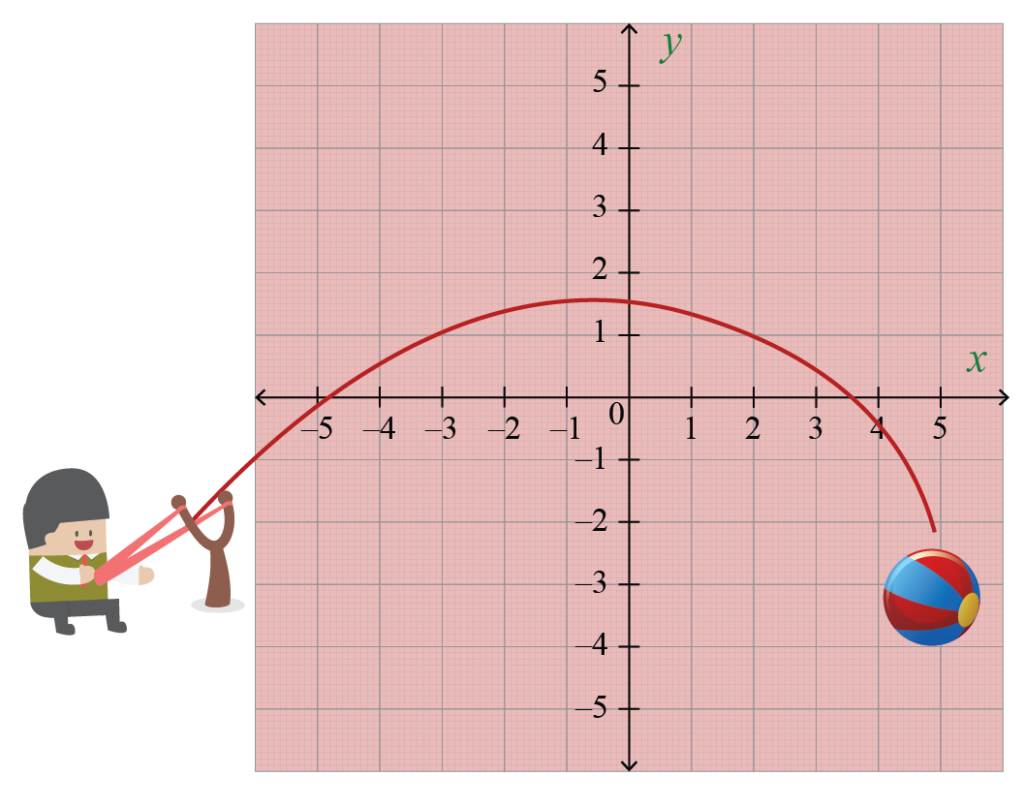
Бросить мяч в воздух. Дуга, по которой он следует, - парабола.. А параболу можно представить квадратным уравнением.
В чем фокус параболы? Один из способов определить параболу - это то, что это набор точек на плоскости, равноудаленных от заданной линии., называется директриса, и заданная точка, назвал фокус.
Как квадратные уравнения применяются в нашей повседневной жизни?
Квадратные уравнения часто используются в повседневной жизни.. Сила тяжести пропорциональна обратному квадрату расстояния от Земли., так снаряды, от теннисного мяча до ракеты, лететь по параболической траектории.
Предположим, вы хотите размешать кофе, центростремительная сила кофе квадратична по своей природе, поэтому, когда вы вынимаете ложку, вы понимаете, что он образует форму параболоида (представьте себе трехмерную параболу).
Квадратные уравнения часто используются в задачах оптимизации как в инженерии, так и в финансах., когда вы хотите минимизировать стоимость определенного товара или максимизировать прибыль, и иногда это можно смоделировать квадратными уравнениями (хотя не всегда).
Способ определения сопротивления резисторов параллельно требует рабочего понимания решения квадратных уравнений, если вы знаете какие-то выводы, поэтому важно иметь правильную комбинацию резисторов, чтобы не повредить важные элементы схемы.
Параболические зеркала и микрофоны используют ту же функцию парабол и, следовательно, параболоидов., то есть они могут концентрировать отражения в одной точке, что дает очень хорошее изображение для телескопа или четкий сигнал с микрофона.
Теперь некоторые по-прежнему повседневные приложения, но в большем масштабе, находятся в ODE 2-го порядка, которые требуют вспомогательного уравнения для решения, которое является квадратным уравнением, и результат которой определяет функцию для всей системы.
Примеры использования этого уравнения - качели, которые используют простое гармоническое движение., как пружины в вашем автомобиле или пружины в большинстве механических устройств на земле.
Происхождение квадратного уравнения
Вавилоняне первыми изобрели квадратные уравнения еще в 2000 году до нашей эры.. Они были нужны им для сельскохозяйственных и ирригационных расчетов..
Греки использовали их позже – Архимед прибег к ним, чтобы найти значение радиуса круга..
Сегодня мы используем их каждый день для расчета площади (размер коробки, гостинная, земельный участок), для определения прибыли от товара (сколько этого товара мне нужно продать, чтобы получить прибыль?) или оценить скорость объекта (если я брошу что-нибудь в тебя – что-то твердое, – как долго то, что я бросаю, попадет в твои руки?)
Причины желания найти решение таких проблем до конца не известны., но мы можем делать предположения.
Например, у них могло быть определенное количество материала, которым можно было заключить прямоугольное поле данной области. Возможно, им нужно было знать, какое идеальное количество материала использовать для этого периметра., или если у них было достаточно.
Какими бы ни были их потребности, у них было решение проблемы. Они записали это шаг за шагом следующим образом:
Икс + и знак равноs; ………………………………………… (1)
хузнак равноa; ……………………………………………. (2)
(1) Найдите половину s.
(2) Возвести в квадрат число, полученное в 1.
(3) Вычтите число, найденное в 2 от a.
(4) Найдите квадратный корень из числа, найденного в 3.
(5) Добавьте число, полученное в 1 к числу, полученному в 4. Это длина одной из сторон.
Выполнение шага 4 была самая сложная часть, хотя известно, что вавилоняне использовали квадратные столы, предположительно содержащий список квадратных чисел, аппроксимировать квадратный корень из числа.
Некоторые историки также приписывают вавилонянам самое первое применение метода Ньютона., который использовался специально для поиска квадратных корней.
Во всем этом интересно то, как квадратная формула (*) возникла из-за такой проблемы. В конце концов, здесь мы не решаем квадратное уравнение, но пара одновременных уравнений (1) а также (2).
Это нетрудно увидеть, используя сегодняшние обозначения. Из (1) мы получаем y = s-x, который при замене на (2) дает:
Икс(s-Икс)знак равноa.
sИкс-Икс2знак равноa.
Икс2-sИкс+aзнак равно0.
таким образом, (1) а также (2) эквивалентны решению квадратного уравнения х2-sx + а = 0. конкретно, это говорит нам, что в этом квадратном уравнении, коэффициент при x является отрицательным из суммы двух решений (уравнение (1) ), а коэффициент при единице - произведение двух решений (уравнение (2) ).



Оставьте ответ
Вы должны авторизоваться или же регистр добавить новый ответ.