Es ist sehr einfach die x- und y-Abschnitte auf einem Graphen zu identifizieren, aber die Studenten häufig kämpfen sie nur unter Verwendung der Gleichung zu finden. jedoch, es erfordert nur einen einfachen Trick:

So finden Sie die x abfangen(s) eine Gleichung, Ersatz in y = 0 und lösen für x.

So finden Sie die y-Achse(s) eine Gleichung, Ersatz in x = 0 und löse für y.

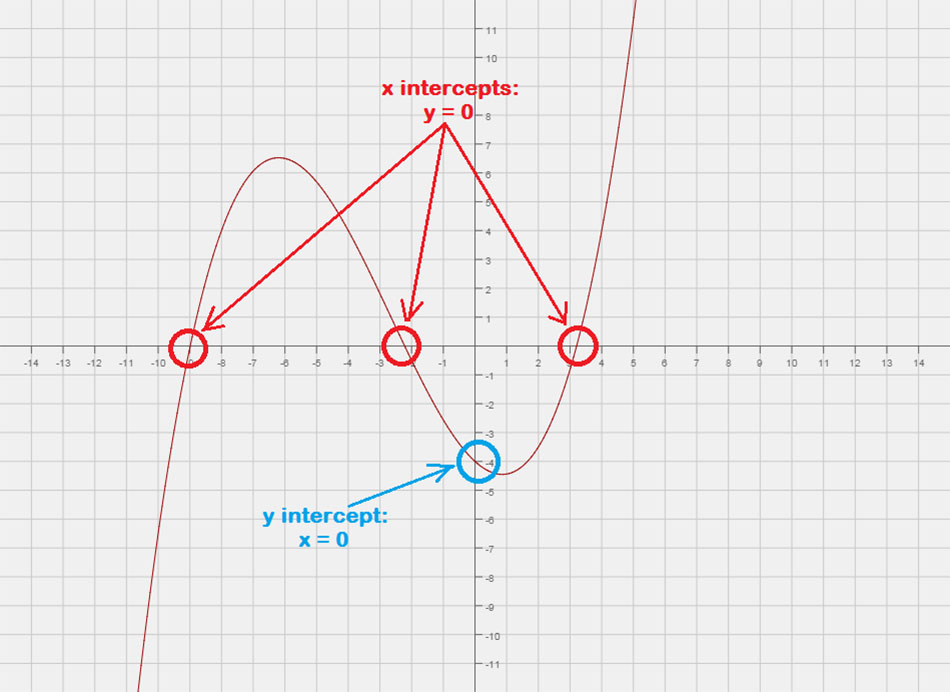
Die X-Abschnitte

Das x-Abschnitte sind Punkte, an denen der Graph einer Funktion oder einer Gleichung die x-Achse der kartesischen Ebene schneidet oder „berührt“.. Sie können sich dies als einen Punkt mit einem y-Wert von Null vorstellen.

• Die x-Achsenabschnitte einer Gleichung finden, Lassen $und=0$ dann löse auf $x$.
• In Punktnotation, es ist geschrieben als \links( {x,0} \Recht)(x,0).

x-Achsenabschnitt einer linearen Funktion oder a Gerade Linie

x-Achsenabschnitte einer Quadratik Funktion oder Parabel

Die Y-Abschnitte

Das y-Achsenabschnitte sind Punkte, an denen der Graph einer Funktion oder einer Gleichung die y-Achse der kartesischen Ebene kreuzt oder „berührt“.. Sie können sich dies als einen Punkt mit einem x-Wert von Null vorstellen.

• Den y-Achsenabschnitt einer Gleichung finden, Lassen $x=0$ dann löse auf $und$.
• In Punktnotation, es ist geschrieben als \links( {0,und} \Recht)(0,und).

y-Achsenabschnitt einer linearen Funktion oder einer geraden Linie

y-Achsenabschnitt einer quadratischen Funktion oder Parabel

Beispiele zum Finden der x- und y-Achsenabschnitte einer Linie, Parabel, und Kreis

Beispiel 1: Aus der Grafik, Beschreiben Sie die x- und y-Achsenabschnitte in Punktnotation.

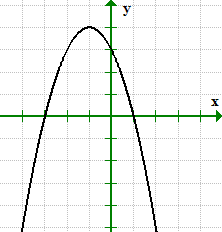
Der Graph schneidet die x-Achse bei x = 1 und x = 3, deshalb, wir können die x-Abschnitte als Punkte schreiben (1,0) und (-3, 0).

Ähnlich, der Graph schneidet die y-Achse bei und = 3. Sein y-Achsenabschnitt kann als Punkt geschrieben werden (0,3).

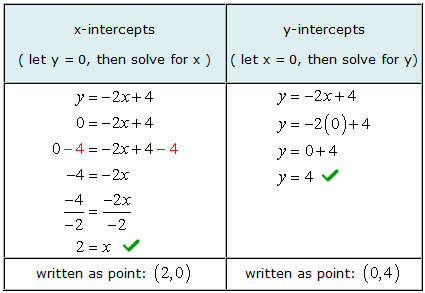
Beispiel 2: Finden Sie die x- und y-Achsenabschnitte der Geraden und = –2x + 4.

Die x-Achsenabschnitte algebraisch finden, wir lassen und = 0 in die Gleichung ein und lösen Sie dann nach Werten von auf x. Auf die gleiche Weise, für y-Achsenabschnitte algebraisch zu finden, wir lassen x = 0 in die Gleichung ein und löse dann auf und.

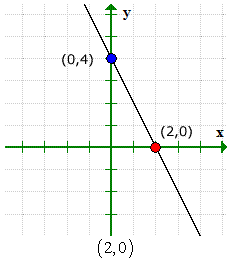
Hier ist die Grafik, um zu überprüfen, ob unsere Antworten richtig sind.

Beispiel 3: Finde die x- und y-Achsenabschnitte der quadratischen Gleichung und = x² - 2x - 3.

Der Graph dieser quadratischen Gleichung ist eine Parabel. Wir erwarten, dass es eine „U“-Form hat, wo es sich entweder nach oben oder unten öffnet.

Lösung für den x-Achsenabschnitt dieses Problems, Du wirst Faktorisiere ein einfaches Trinom. Dann setzen Sie jeden Binomialfaktor gleich Null und lösen nach x auf.

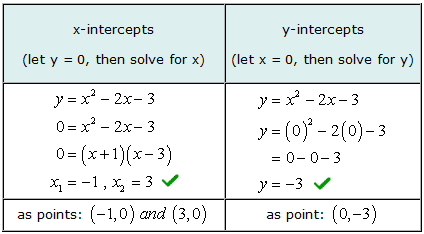
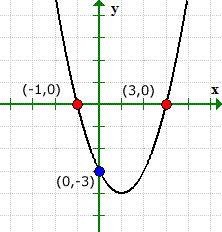
Unsere gelösten Werte für x- und y-Achsenabschnitte stimmen mit der grafischen Lösung überein.

Beispiel 4: Finde die x- und y-Achsenabschnitte der quadratischen Gleichung und = 3x² + 1.

Dies ist ein Beispiel, bei dem der Graph der Gleichung einen y-Achsenabschnitt, aber keinen x-Achsenabschnitt hat.

• Lassen Sie uns zuerst den y-Achsenabschnitt finden, weil es extrem einfach ist! Stecken Sie x = ein 0 dann löse nach y auf.

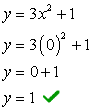
• Nun zum x-Achsenabschnitt. Stecken Sie y = ein 0, und lösen für x.

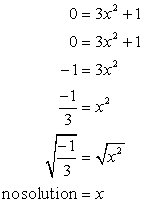
Die Quadratwurzel einer negativen Zahl ist imaginär. Dies legt nahe, dass diese Gleichung hat nicht ein x-Achsenabschnitt!

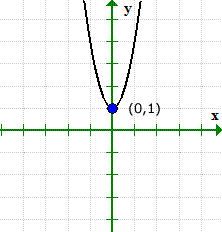
Die Grafik kann überprüfen, was vor sich geht. Beachten Sie, dass der Graph die y-Achse bei kreuzte (0,1), aber nie mit der x-Achse.

Beispiel 5: Finde die x- und y-Achsenabschnitte des Kreises (x + 4)² + (und + 2)² = 8.

Dies ist ein gutes Beispiel, um zu veranschaulichen, dass es für den Graphen einer Gleichung möglich ist, x-Abschnitte, aber keine y-Abschnitte zu haben.

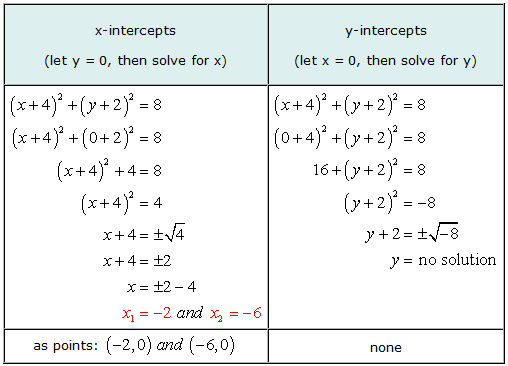
Beim Auflösen nach y, Wir kamen in die Situation, in der wir versuchten, die Quadratwurzel einer negativen Zahl zu ziehen. Die Antwort ist imaginär, so, keine Lösung. Das bedeutet, dass die Gleichung keine y-Achsenabschnitte hat.

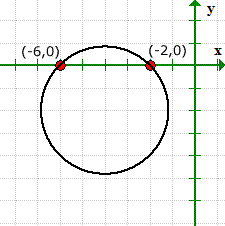
Die Grafik bestätigt, dass wir mit den Werten unserer x-Abschnitte richtig liegen, und es hat keine y-Achsenabschnitte.

Kredit:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/