Quali sono gli scenari di vita reale che coinvolgono le equazioni quadratiche??
Ci sono molte situazioni reali che coinvolgono quadratiche e parabole. Lanciare una palla, sparare con un cannone, tuffarsi da una piattaforma, e colpire una pallina da golf sono tutti esempi di situazioni che possono essere simulate utilizzando funzioni quadratiche.
L'equazione quadratica è praticamente usata in astronomia, matematica, ingegneria, medicinale, finanza, silvicoltura, scienza o ricerca, eccetera. In qualsiasi campo, se c'è un'attività accademica o di ricerca, è probabile che ci sia un sistema di equazioni che potrebbe richiedere un'equazione quadratica per essere risolta.
Per la vita ordinaria, senza l'uso di alcun materiale accademico, la matematica o le equazioni non sono necessarie; e, perciò, non è richiesta un'equazione quadratica.
Rimarrai sorpreso dal numero di applicazioni che utilizzano equazioni quadratiche.
Lancia una palla in aria. L'arco che segue è una parabola. E una parabola può essere rappresentata da un'equazione quadratica.
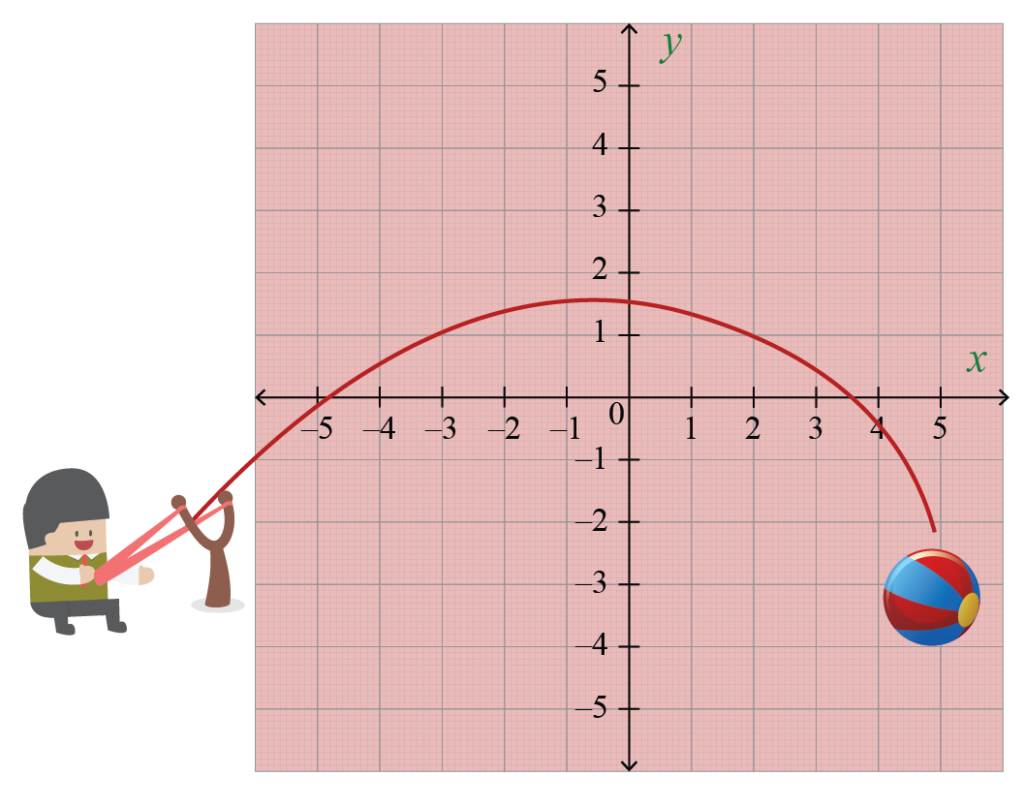
Qual è il fulcro di una parabola?? Un modo per definire una parabola è che sia l'insieme dei punti nel piano equidistanti da una retta data, chiamata la direttrice, e un dato punto, chiamato il focus.
Come vengono applicate le equazioni quadratiche nella nostra vita quotidiana??
Le equazioni quadratiche sono spesso usate nella vita di tutti i giorni. La forza di gravità è proporzionale all'inverso del quadrato della distanza dalla Terra, quindi proiettili, da una pallina da tennis a un razzo, volare lungo una traiettoria parabolica.
Supponi di voler mescolare il caffè, la forza centripeta del caffè è di natura quadratica, quindi quando togli il cucchiaio, ti rendi conto che forma una forma paraboloide (immagina una parabola tridimensionale).
Le equazioni quadratiche sono spesso utilizzate nei problemi di ottimizzazione sia in ingegneria che in finanza, quando vuoi minimizzare il costo di un particolare bene o massimizzare il profitto, e a volte questo può essere modellato da equazioni quadratiche (anche se non sempre).
Il modo per determinare la resistenza dei resistori in parallelo richiede una comprensione pratica della risoluzione di equazioni quadratiche, se conosci qualche conclusione, quindi è importante avere la giusta combinazione di resistori in modo da non distruggere importanti elementi del circuito.
Specchi parabolici e microfoni utilizzano la stessa caratteristica delle parabole e quindi dei paraboloidi, che è che possono concentrare le riflessioni in un punto, che fornisce un'immagine molto buona per un telescopio o un segnale chiaro da un microfono.
Ora alcune applicazioni ancora quotidiane, ma su scala più ampia, sono in ODE di 2° ordine, che richiedono un'equazione ausiliaria da risolvere, che è un'equazione quadratica, e il cui risultato determina la funzione per l'intero sistema.
Esempi di usi di questa equazione sono le oscillazioni che utilizzano il movimento armonico semplice, come le molle della tua auto o le molle della maggior parte dei dispositivi meccanici a terra.
Origine dell'equazione quadratica
I babilonesi furono i primi a inventare equazioni quadratiche già nel 2000 a.C.. Ne avevano bisogno per i calcoli agricoli e di irrigazione.
I greci li usarono in seguito – Archimede ricorse a loro per trovare il valore del raggio di un cerchio.
Oggi li usiamo tutti i giorni per calcolare l'area (le dimensioni di una scatola, soggiorno, un appezzamento di terreno), determinare il profitto di una merce (quanto di questa merce devo vendere per realizzare un profitto??) o per stimare la velocità di un oggetto (se ti lancio qualcosa – qualcosa di solido, – quanto tempo ci vorrà prima che quello che lancio finisca nelle tue mani?)
Le ragioni per voler trovare una soluzione a tali problemi non sono completamente note, ma possiamo fare delle ipotesi.
Per esempio, potrebbero aver avuto una certa quantità di materiale con cui racchiudere un campo rettangolare di una data area. Forse avevano bisogno di sapere quale fosse la quantità ideale di materiale da utilizzare per quel perimetro, o se ne avessero abbastanza.
Qualunque siano le loro esigenze, avevano una soluzione al problema. L'hanno scritto passo dopo passo come segue:
X + e =S; ………………………………………… (1)
xy=un'; ……………………………………………. (2)
(1) Trova la metà di S.
(2) Eleva al quadrato il numero ottenuto in 1.
(3) Sottrai il numero trovato in 2 di un'.
(4) Trova la radice quadrata del numero trovato in 3.
(5) Aggiungi il numero ottenuto in 1 al numero ottenuto in 4.Questa è la lunghezza di uno dei lati.
Esecuzione del passaggio 4 è stata la parte più difficile, anche se si sa che i Babilonesi usavano tavole quadrate, presumibilmente contenente un elenco di numeri quadrati, approssimare la radice quadrata di un numero.
Alcuni storici attribuiscono anche ai Babilonesi la primissima applicazione del metodo di Newton, che è stato usato specificamente per trovare radici quadrate.
La cosa interessante di tutto questo è come la formula quadratica (*) nasce da un tale problema. Dopotutto, non stiamo risolvendo un'equazione quadratica qui, ma una coppia di equazioni simultanee (1) e (2).
Questo non è difficile da vedere, usando le notazioni di oggi. A partire dal (1) otteniamo y=s-x, che quando sostituito in (2) dà:
X(S-X)=un'.
SX-X2=un'.
X2-SX+un'=0.
così, (1) e (2) sono equivalenti a risolvere l'equazione quadratica x2-sx+a=0. In particolare, questo ci dice che in questa equazione quadratica, il coefficiente di x è il negativo della somma delle due soluzioni (equazione (1) ), e il coefficiente di uno è il prodotto delle due soluzioni (equazione (2) ).



Lascia una risposta
Devi accesso o Registrati per aggiungere una nuova risposta.