Wat is mechanische energie? Ik heb een sluitende definitie
Wat is mechanische energie
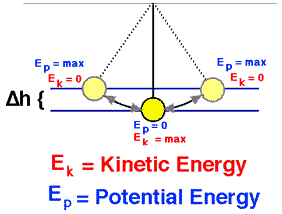 natuurkunde, mechanische energie (Emecha) is de energie geassocieerd met de beweging en positie van een object meestal in een krachtveld (bv. zwaartekracht veld). Mechanische energie (en ook de thermische energie) kan worden onderverdeeld in twee categorieën:, voorbijgaand en opgeslagen. Tijdelijke energie is energie in beweging, dat is, energie wordt van de ene plaats naar de andere overgebracht. Opgeslagen energie is de energie die zich in een stof of object bevindt. Voorbijgaande mechanische energie wordt gewoonlijk aangeduid als: werk. Opgeslagen mechanische energie bestaat in een van de twee vormen:: kinetisch of potentieel:
natuurkunde, mechanische energie (Emecha) is de energie geassocieerd met de beweging en positie van een object meestal in een krachtveld (bv. zwaartekracht veld). Mechanische energie (en ook de thermische energie) kan worden onderverdeeld in twee categorieën:, voorbijgaand en opgeslagen. Tijdelijke energie is energie in beweging, dat is, energie wordt van de ene plaats naar de andere overgebracht. Opgeslagen energie is de energie die zich in een stof of object bevindt. Voorbijgaande mechanische energie wordt gewoonlijk aangeduid als: werk. Opgeslagen mechanische energie bestaat in een van de twee vormen:: kinetisch of potentieel:
- Potentiële energie. Potentiële energie, u, wordt gedefinieerd als de energie die is opgeslagen in een object dat wordt onderworpen aan een conservatieve kracht. Veel voorkomende typen zijn de zwaartekracht potentiële energie van een object die afhangt van de massa en de afstand tot het zwaartepunt van een ander object.
- Kinetische energie. De kinetische energie, K, wordt gedefinieerd als de energie die in een object is opgeslagen vanwege zijn beweging. Het hangt af van de snelheid van een object en is het vermogen van een bewegend object om aan andere objecten te werken wanneer het ermee in botsing komt.
Behoud van mechanische energie
Eerst het principe van de Behoud van mechanische energie werd vermeld:
De totale mechanische energie (gedefinieerd als de som van zijn potentiële en kinetische energie) van een deeltje waarop alleen conservatieve krachten werken is constant.
Zie ook: Behoud van mechanische energie
Een geïsoleerd systeem is er een waarin geen externe kracht veroorzaakt energieveranderingen. Als alleen conservatieve krachten handelen op een object en u is de potentiële energie functie voor de totale conservatieve kracht, dan
Emecha = U + K
de potentiële energie, u, hangt af van de positie van een object dat onderworpen is aan een conservatieve kracht.
Het wordt gedefinieerd als het vermogen van het object om werk te doen en neemt toe naarmate het object in de tegenovergestelde richting van de richting van de kracht wordt bewogen.
de potentiële energie geassocieerd met een systeem bestaande uit de aarde en een nabijgelegen deeltje is zwaartekracht potentiële energie.
De kinetische energie, K, hangt af van de snelheid van een object en is het vermogen van een bewegend object om aan andere objecten te werken wanneer het ermee in botsing komt.
K = ½ mv2
De bovengenoemde definitie (Emecha = U + K) gaat ervan uit dat het systeem vrij van wrijving en andere niet-conservatieve krachten. Het verschil tussen een conservatieve en een niet-conservatieve kracht is dat wanneer een conservatieve kracht een object van het ene punt naar het andere beweegt, het werk van de conservatieve kracht is onafhankelijk van het pad.
In elke echte situatie, wrijvingskrachten en andere niet-conservatieve krachten zijn aanwezig, maar in veel gevallen zijn hun effecten op het systeem zo klein dat het principe van: behoud van mechanische energie kan worden gebruikt als een eerlijke benadering. De wrijvingskracht is bijvoorbeeld een niet-conservatieve kracht, omdat het werkt om de mechanische energie in een systeem te verminderen.
Merk op dat niet-conservatieve krachten de mechanische energie niet altijd te verminderen. Een niet-conservatieve kracht verandert de mechanische energie, er zijn krachten die de totale mechanische energie verhogen, zoals de kracht geleverd door een motor of motoren, Ook een niet-conservatieve kracht.
Blok glijden van een wrijvingsloze helling
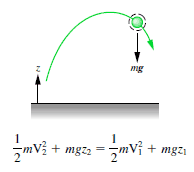
De 1 kg blok begint een hoogte H (laten we zeggen 1 m) boven de grond, met potentiële energie mgH en kinetische energie dat is gelijk aan 0. Het glijdt naar de grond (zonder wrijving) en arriveert zonder potentiële energie en kinetische energie K = ½ mv2. Bereken de snelheid van het blok op de grond en zijn kinetische energie.
Emecha = U + K = const
=> mv2 = mgH
=> v = √2gH = 4.43 Mevrouw
=> K2 = ½ x 1 kg x (4.43 Mevrouw)2 = 19.62 kg.m2.s-2 = 19.62 J
Slinger
 neem aan dat de slinger (bal met massa m opgehangen aan een touwtje van lengte L die we hebben opgetrokken zodat de bal een hoogte heeft H < L boven het laagste punt op de boog van zijn uitgerekte snaarbeweging. De slinger is onderworpen aan de conservatieve zwaartekracht waar wrijvingskrachten zoals luchtweerstand en wrijving bij het draaipunt verwaarloosbaar zijn.
neem aan dat de slinger (bal met massa m opgehangen aan een touwtje van lengte L die we hebben opgetrokken zodat de bal een hoogte heeft H < L boven het laagste punt op de boog van zijn uitgerekte snaarbeweging. De slinger is onderworpen aan de conservatieve zwaartekracht waar wrijvingskrachten zoals luchtweerstand en wrijving bij het draaipunt verwaarloosbaar zijn.
We bevrijden het van rust. Hoe snel gaat het onderaan?
De slinger bereikt grootste kinetische energie en minste potentiële energie wanneer in de verticale positie, omdat het de grootste snelheid heeft en op dit punt het dichtst bij de aarde is. Anderzijds, het zal zijn . hebben minste kinetische energie en grootste potentiële energie bij de extreme posities van zijn schommel, omdat het geen snelheid heeft en op deze punten het verst van de aarde verwijderd is.
Als de amplitude beperkt is tot kleine schommelingen, de periode T van een eenvoudige slinger, de tijd die nodig is voor een volledige cyclus, is:
waar L is de lengte van de slinger en g is de lokale versnelling van de zwaartekracht. Voor kleine schommels is de schommelperiode ongeveer hetzelfde voor schommels van verschillende grootte. Dat is, de periode is onafhankelijk van de amplitude.



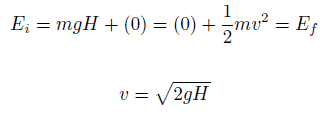
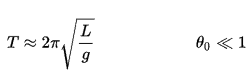
Laat een antwoord achter
Je moet Log in of registreren om een nieuw antwoord toe te voegen.