O que é a energia mecânica? Eu preciso de uma definição abrangente
O que é a energia mecânica
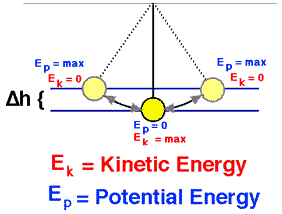 na física, energia mecânica (Emech) é a energia associada ao movimento e posição de um objeto geralmente em algum campo de força (por exemplo. campo gravitacional). Energia mecânica (e também a energia térmica) podem ser separados em duas categorias, transitório e armazenado. Energia transitória é energia em movimento, isso é, energia sendo transferida de um lugar para outro. Energia armazenada é a energia contida em uma substância ou objeto. A energia mecânica transitória é comumente referida como trabalhos. A energia mecânica armazenada existe em uma de duas formas: cinética ou potencial:
na física, energia mecânica (Emech) é a energia associada ao movimento e posição de um objeto geralmente em algum campo de força (por exemplo. campo gravitacional). Energia mecânica (e também a energia térmica) podem ser separados em duas categorias, transitório e armazenado. Energia transitória é energia em movimento, isso é, energia sendo transferida de um lugar para outro. Energia armazenada é a energia contida em uma substância ou objeto. A energia mecânica transitória é comumente referida como trabalhos. A energia mecânica armazenada existe em uma de duas formas: cinética ou potencial:
- Energia potencial. Energia potencial, o, é definido como a energia armazenada em um objeto submetido a uma força conservadora. Os tipos comuns incluem a energia potencial gravitacional de um objeto que depende de sua massa e de sua distância do centro de massa de outro objeto.
- Energia cinética. A energia cinética, K, é definido como a energia armazenada em um objeto por causa de seu movimento. Depende da velocidade de um objeto e é a capacidade de um objeto em movimento de trabalhar em outros objetos quando colide com eles.
Conservação de Energia Mecânica
Primeiro, o princípio do Conservação de Energia Mecânica foi declarado:
A energia mecânica total (definido como a soma de suas energias potenciais e cinéticas) de uma partícula sendo influenciada apenas por forças conservativas é constante.
Veja também: Conservação de Energia Mecânica
Um sistema isolado é aquele em que nenhuma força externa causa mudanças de energia. Se apenas forças conservadoras agir sobre um objeto e o é o energia potencial função para a força conservadora total, então
Emech = U + K
A energia potencial, o, depende da posição de um objeto submetido a uma força conservadora.
É definido como a capacidade do objeto de fazer trabalho e é aumentada conforme o objeto é movido na direção oposta da direção da força.
A energia potencial associado a um sistema que consiste na Terra e uma partícula próxima é energia potencial gravitacional.
A energia cinética, K, depende da velocidade de um objeto e é a capacidade de um objeto em movimento de trabalhar em outros objetos quando colide com eles.
K = ½ mv2
A definição acima mencionada (Emech = U + K) assume que o sistema é livre de atrito e outro forças não conservadoras. A diferença entre uma força conservadora e uma força não conservadora é que quando uma força conservadora move um objeto de um ponto a outro, o trabalho feito pela força conservadora é independente do caminho.
Em qualquer situação real, forças de fricção e outras forças não conservadoras estão presentes, mas em muitos casos seus efeitos sobre o sistema são tão pequenos que o princípio de conservação de energia mecânica pode ser usado como uma aproximação justa. Por exemplo, a força de atrito é uma força não conservadora, porque atua para reduzir a energia mecânica em um sistema.
Observe que as forças não conservativas nem sempre reduzem a energia mecânica. Uma força não conservadora altera a energia mecânica, existem forças que aumentam a energia mecânica total, como a força fornecida por um motor ou motor, também é uma força não conservadora.
Bloco deslizando por uma encosta inclinada sem atrito
o 1 bloco de kg começa com uma altura H (deixe dizer 1 m) sobre o chão, com energia potencial mgH e energia cinética isso é igual a 0. Ele desliza para o chão (sem atrito) e chega sem energia potencial e energia cinética K = ½ mv2. Calcule a velocidade do bloco no solo e sua energia cinética.
Emech = U + K = const
=> ½ mv2 = mgH
=> v = √2gH = 4.43 Senhora
=> K2 = ½ x 1 kg x (4.43 Senhora)2 = 19.62 kg.m2.s-2 = 19.62 J
Pêndulo
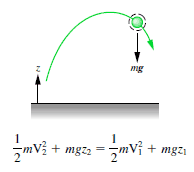
 Assume a pêndulo (bola de massa m suspensa em uma corda de comprimento eu que puxamos para cima de modo que a bola esteja na altura H < eu acima de seu ponto mais baixo no arco de seu movimento de corda esticada. O pêndulo está sujeito ao força gravitacional conservadora onde as forças de atrito como arrasto de ar e fricção no pivô são insignificantes.
Assume a pêndulo (bola de massa m suspensa em uma corda de comprimento eu que puxamos para cima de modo que a bola esteja na altura H < eu acima de seu ponto mais baixo no arco de seu movimento de corda esticada. O pêndulo está sujeito ao força gravitacional conservadora onde as forças de atrito como arrasto de ar e fricção no pivô são insignificantes.
Nós o liberamos do descanso. Quão rápido está indo no fundo?
O pêndulo atinge maior energia cinética e menos energia potencial quando no posição vertical, porque terá a maior velocidade e estará mais próximo da Terra neste ponto. Por outro lado, terá seu menos energia cinética e maior energia potencial no posições extremas de seu swing, porque tem velocidade zero e está mais distante da Terra nesses pontos.
Se a amplitude é limitada a pequenas oscilações, o período T de um pêndulo simples, o tempo gasto para um ciclo completo, é:
Onde eu é o comprimento do pêndulo e g é a aceleração local da gravidade. Para pequenas oscilações, o período de oscilação é aproximadamente o mesmo para oscilações de tamanhos diferentes. Isso é, o período é independente da amplitude.



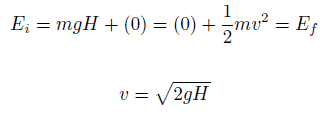
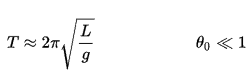
Deixe uma resposta
Você deve Conecte-se ou registro para adicionar uma nova resposta.