Что такое механическая энергия? Мне нужно исчерпывающее определение
Что такое механическая энергия
 В физике, механическая энергия (Емех) это энергия, связанная с движение а также должность объекта обычно в некотором силовом поле (например. гравитационное поле). Механическая энергия (а также тепловая энергия) можно разделить на две категории, переходный и сохраняемый. Переходная энергия – это энергия в движении, то есть, энергия переносится из одного места в другое. Запасенная энергия — это энергия, содержащаяся в веществе или объекте.. Переходную механическую энергию обычно называют Работа. Запасенная механическая энергия существует в одной из двух форм: кинетический или же потенциал:
В физике, механическая энергия (Емех) это энергия, связанная с движение а также должность объекта обычно в некотором силовом поле (например. гравитационное поле). Механическая энергия (а также тепловая энергия) можно разделить на две категории, переходный и сохраняемый. Переходная энергия – это энергия в движении, то есть, энергия переносится из одного места в другое. Запасенная энергия — это энергия, содержащаяся в веществе или объекте.. Переходную механическую энергию обычно называют Работа. Запасенная механическая энергия существует в одной из двух форм: кинетический или же потенциал:
- Потенциальная энергия. Потенциальная энергия, U, определяется как энергия, запасенная в объекте, на который действует консервативная сила. Общие типы включают гравитационную потенциальную энергию объекта, которая зависит от его массы и расстояния от центра масс другого объекта..
- Кинетическая энергия. Кинетическая энергия, K, определяется как энергия, запасенная в объекте из-за его движения. Она зависит от скорости объекта и представляет собой способность движущегося объекта совершать работу с другими объектами при столкновении с ними..
Сохранение механической энергии
Во-первых, принцип Сохранение механической энергии было заявлено:
Полная механическая энергия (определяется как сумма его потенциальной и кинетической энергий) на частицу действуют только консервативные силы постоянно.
Смотрите также: Сохранение механической энергии
Изолированная система тот, в котором нет внешней силы вызывает энергетические изменения. Если только консервативные силы воздействовать на объект и U это потенциальная энергия функция полной консервативной силы, тогда
Емех = U + K
Потенциальная энергия, U, зависит от положения объекта, на который действует консервативная сила.
Она определяется как способность объекта совершать работу и увеличивается по мере того, как объект перемещается в направлении, противоположном направлению действия силы..
Потенциальная энергия связана с системой, состоящей из Земли и соседней частицы. гравитационно потенциальная энергия.
Кинетическая энергия, K, зависит от скорости объекта и представляет собой способность движущегося объекта совершать работу с другими объектами при столкновении с ними.
К = мв2
Вышеупомянутое определение (Емех = U + K) предполагает, что система свободный от трения и другие неконсервативные силы. Разница между консервативной и неконсервативной силой заключается в том, что когда консервативная сила перемещает объект из одной точки в другую, работа консервативной силы не зависит от пути.
В любой реальной ситуации, силы трения и другие неконсервативные силы присутствуют, но во многих случаях их влияние на систему настолько мало, что принцип сохранение механической энергии можно использовать как справедливое приближение. Например, сила трения является неконсервативной силой., потому что он уменьшает механическую энергию в системе.
Обратите внимание, что неконсервативные силы не всегда уменьшают механическую энергию.. Неконсервативная сила изменяет механическую энергию, есть силы, увеличивающие полную механическую энергию, как сила, обеспечиваемая мотором или двигателем, также является неконсервативной силой.
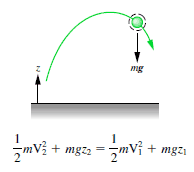
Блок скользит по наклонному склону без трения
В 1 кг блок начинается с высоты H (пусть говорят 1 м) выше земли, с потенциальная энергия мгH а также кинетическая энергия что равно 0. Он скользит на землю (без трения) и прибывает без потенциальной энергии и кинетической энергии К = мв2. Вычислите скорость блока на земле и его кинетическую энергию.
Емех = U + К = константа
знак равно> ½ мв2 = мгН
знак равно> v = √2gH = 4.43 РС
знак равно> K2 = ½ х 1 кг х (4.43 РС)2 знак равно 19.62 кг.м2.s-2 знак равно 19.62 J
Маятник
 Предположим, маятник (шар массой m подвешен на нити длиной L что мы подтянули так, что мяч в высоту ЧАС < L выше его нижней точки на дуге движения натянутой струны. Маятник подвергается воздействию консервативная гравитационная сила где силы трения, такие как сопротивление воздуха и трение в шарнире, пренебрежимо малы.
Предположим, маятник (шар массой m подвешен на нити длиной L что мы подтянули так, что мяч в высоту ЧАС < L выше его нижней точки на дуге движения натянутой струны. Маятник подвергается воздействию консервативная гравитационная сила где силы трения, такие как сопротивление воздуха и трение в шарнире, пренебрежимо малы.
Мы освобождаем его от покоя. Как быстро это происходит внизу?
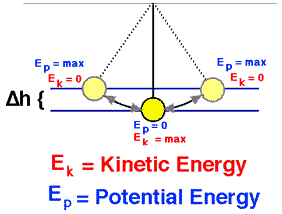
Маятник достигает наибольшая кинетическая энергия а также наименьшая потенциальная энергия когда в Вертикальная позиция, потому что он будет иметь наибольшую скорость и будет ближе всего к Земле в этой точке. С другой стороны, у него будет свой наименьшая кинетическая энергия а также наибольшая потенциальная энергия на крайние позиции его колебания, потому что он имеет нулевую скорость и находится дальше всего от Земли в этих точках.
Если амплитуда ограничена небольшими колебаниями, Период T простого маятника, время, необходимое для полного цикла, является:
где L длина маятника и г это местное ускорение силы тяжести. Для малых качелей период качания примерно одинаков для качелей разного размера.. То есть, период не зависит от амплитуды.



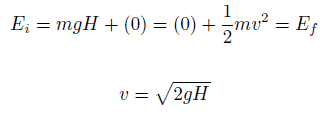
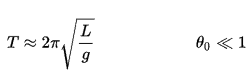
Оставьте ответ
Вы должны авторизоваться или же регистр добавить новый ответ.