Je! Ni Nini Hali ya Maisha Halisi inayohusisha Mlinganisho wa Quadratic?
Kuna hali nyingi halisi zinazojumuisha quadratics na parabolas. Kutupa mpira, kupiga bunduki, kupiga mbizi kwenye jukwaa, na kupiga mpira wa gofu ni mifano yote ya hali ambazo zinaweza kuigwa kwa kutumia kazi za quadratic.
Mlinganyo wa quadratic hutumiwa kwa vitendo katika unajimu, hisabati, Uhandisi, dawa, fedha, misitu, sayansi au utafiti, na kadhalika. Katika uwanja wowote, ikiwa kuna shughuli ya kitaaluma au utafiti, kuna uwezekano wa kuwa na mfumo wa equations ambao unaweza kuhitaji hesabu ya quadratic kutatua.
Kwa maisha ya kawaida, bila matumizi ya vifaa vyovyote vya masomo, hisabati au equations hazihitajiki; na, kwa hivyo, equation ya quadratic haihitajiki.
Utashangazwa na idadi ya programu zinazotumia milinganyo ya quadratic.
Tupa mpira hewani. Safu inayofuata ni parabola. Na parabola inaweza kuwakilishwa na equation ya quadratic.
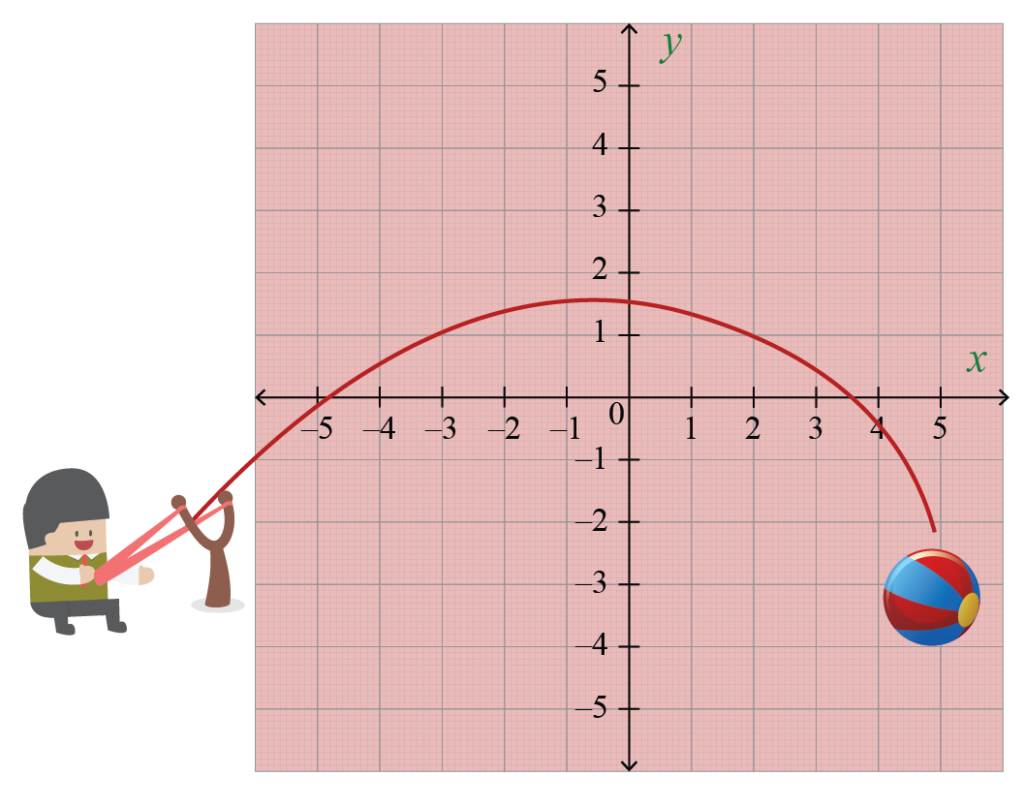
Nini lengo la parabola? Njia moja ya kufafanua parabola ni kwamba ni seti ya alama kwenye usawa wa ndege kutoka kwa mstari uliopeanwa., inayoitwa directrix, na nukta fulani, inayoitwa umakini.
Jinsi milinganyo ya quadratic inatumika katika maisha yetu ya kila siku?
Milinganyo ya quadratic mara nyingi hutumiwa katika maisha ya kila siku. Nguvu ya mvuto ni sawa na mraba wa inverse wa umbali kutoka Dunia, hivyo projectiles, kutoka mpira wa tenisi hadi roketi, kuruka kando ya trafiki ya kifumbo.
Tuseme unataka kuchochea kahawa, nguvu ya centripetal ya kahawa ni asili ya quadratic, kwa hivyo unapoondoa kijiko, unatambua kuwa huunda sura ya paraboloid (fikiria parabola ya pande tatu).
Usawa wa Quadratic hutumiwa mara nyingi katika shida za uboreshaji katika uhandisi na fedha, wakati unataka kupunguza gharama ya faida fulani au kuongeza faida, na wakati mwingine hii inaweza kuigwa na equations quadratic (ingawa sio kila wakati).
Njia ya kuamua upinzani wa vipinga sambamba inahitaji uelewa wa kufanya kazi wa kutatua hesabu za quadratic, ikiwa unajua hitimisho, kwa hivyo ni muhimu kuwa na mchanganyiko sahihi wa vipinga ili usiharibu vitu muhimu vya mzunguko.
Vioo vya sauti na maikrofoni hutumia huduma sawa ya paraboli na kwa hivyo paraboloids, ambayo ni kwamba wanaweza kuzingatia tafakari wakati mmoja, ambayo inatoa picha nzuri sana kwa darubini au ishara wazi kutoka kwa kipaza sauti.
Sasa baadhi ya maombi ya kila siku bado, lakini kwa kiwango kikubwa zaidi, ziko katika ODE za mpangilio wa 2, ambayo yanahitaji equation msaidizi kutatua, ambayo ni mlinganyo wa quadratic, na ambaye matokeo yake huamua kazi ya mfumo mzima.
Mifano ya matumizi ya mlingano huu ni bembea zinazotumia mwendo rahisi wa sauti, kama vile chemchemi za gari lako au chemchemi katika vifaa vingi vya kiufundi vilivyo chini.
Asili ya Quadratic Equation
Wababeli walikuwa wa kwanza kubuni hesabu za quadratic huko 2000BC. Waliwahitaji kwa mahesabu ya kilimo na umwagiliaji.
Wagiriki waliwatumia baadaye – Archimedes aliwasiliana nao kupata thamani ya eneo la duara.
Leo tunazitumia kila siku kuhesabu eneo (saizi ya sanduku, sebule, shamba), kuamua faida ya bidhaa (ni kiasi gani cha bidhaa hii ninahitaji kuuza ili kupata faida?) au kukadiria kasi ya kitu (nikikutupia kitu – kitu kigumu, – itachukua muda gani kwa kile ninachotupa kuishia mikononi mwako?)
Sababu za kutaka kupata suluhisho kwa shida kama hizo hazijulikani kabisa, lakini tunaweza kufanya makisio.
Kwa mfano, wanaweza kuwa na kiasi fulani cha nyenzo ambazo zinaweza kufunika uwanja wa mstatili wa eneo fulani. Labda walihitaji kujua ni kiwango kipi bora cha nyenzo cha kutumia kwa mzunguko huo, au ikiwa walikuwa na ya kutosha.
Chochote mahitaji yao, walikuwa na suluhisho la shida. Waliiandika hatua kwa hatua kama ifuatavyo:
x + Y =s; ………………………………………… (1)
xy=a; ……………………………………………. (2)
(1) Pata nusu ya s.
(2) Mraba nambari iliyopatikana katika 1.
(3) Ondoa nambari inayopatikana katika 2 na a.
(4) Pata mzizi wa mraba wa nambari inayopatikana katika 3.
(5) Ongeza nambari iliyopatikana katika 1 kwa nambari iliyopatikana katika 4. Huu ni urefu wa moja ya pande.
Kufanya hatua 4 ilikuwa sehemu ngumu zaidi, ingawa Wababeli wanajulikana kuwa walitumia meza za mraba, labda ina orodha ya nambari za mraba, kukadiria mizizi ya mraba ya nambari.
Wanahistoria wengine pia wanasema kwa Wababeli matumizi ya kwanza kabisa ya njia ya Newton, ambayo ilitumika haswa kupata mizizi ya mraba.
Jambo la kufurahisha juu ya haya yote ni jinsi fomati ya quadratic (∗) ilitoka kwa shida kama hiyo. Baada ya yote, hatujatatua mlinganyo wa nambari hapa, lakini jozi ya hesabu za wakati huo huo (1) na (2).
Hii sio ngumu kuona, kutumia nukuu za leo. Kutoka (1) tunapata y = s-x, ambayo ilibadilishwa kuwa (2) anatoa:
x(s-x)=a.
sx-x2=a.
x2-sx+a=0.
Kwa hivyo, (1) na (2) ni sawa na kutatua equation ya quadratic x2-sx + a = 0. Hasa, hii inatuambia kuwa katika hesabu hii ya nambari, mgawo wa x ni hasi ya jumla ya suluhisho mbili (equation (1) ), na mgawo wa moja ni bidhaa ya suluhisho mbili (equation (2) ).



Acha jibu
Lazima Ingia au kujiandikisha kuongeza jibu jipya.