Diskrete Wahrscheinlichkeitsverteilungen

Mehrere spezialisierte diskrete Wahrscheinlichkeitsverteilungen sind für bestimmte Anwendungen nützlich. Für Geschäftsanwendungen, drei häufig verwendete diskrete Verteilungen sind:

• Binomial

• Geometrisch

• Poisson

Sie verwenden die Binomialverteilung um Wahrscheinlichkeiten für einen Prozess zu berechnen, bei dem bei jedem Versuch nur eines von zwei möglichen Ergebnissen auftreten kann. Das geometrische Verteilung hängt mit der Binomialverteilung zusammen; Sie verwenden die geometrische Verteilung, um die Wahrscheinlichkeit zu bestimmen, dass eine bestimmte Anzahl von Versuchen stattfindet, bevor der erste Erfolg eintritt. Du kannst den ... benutzen Poisson-Verteilung um die Wahrscheinlichkeit zu messen, dass eine bestimmte Anzahl von Ereignissen während eines bestimmten Zeitraums eintritt.

Kontinuierliche Wahrscheinlichkeitsverteilungen

Viele kontinuierliche Distributionen können für Geschäftsanwendungen verwendet werden; zwei der am häufigsten verwendeten sind:

• Uniform

• Normal

Das gleichmäßige Verteilung ist nützlich, da es Variablen darstellt, die gleichmäßig über ein bestimmtes Intervall verteilt sind. Beispielsweise, wenn die Zeitdauer bis zum Eintreffen des nächsten defekten Teils am Fließband ebenfalls zwischen einer und zehn Minuten liegen dürfte, dann können Sie die Gleichverteilung verwenden, um Wahrscheinlichkeiten für die Zeit bis zum Eintreffen des nächsten defekten Teils zu berechnen.

Die glockenförmige Kurve der Normalverteilung.

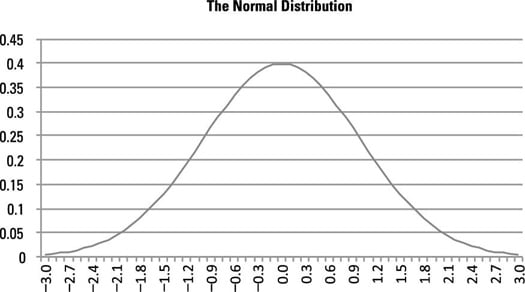
Das Normalverteilung ist für eine breite Palette von Anwendungen in vielen Disziplinen nützlich. Bei Geschäftsanwendungen, Von Variablen wie Aktienrenditen wird oft angenommen, dass sie der Normalverteilung folgen. Die Normalverteilung ist gekennzeichnet durch a glockenförmige Kurve, und Bereiche unter dieser Kurve stellen Wahrscheinlichkeiten dar. Hier ist die glockenförmige Kurve dargestellt.

KREDIT:

Durch Alan Anderson

www.dummies.com/education/math/business-statistics/differentiate-between-discrete-and-continuous-probability-distributions