Es muy simple de identificar a las X e Y intercepta en un gráfico, pero los estudiantes con frecuencia tienen dificultades para encontrarlos utilizando sólo la ecuación. sin embargo, que sólo requiere un simple truco:

Para encontrar la x en la intersección(s) de una ecuación, sustituto en y = 0 y resolver para x.

Para encontrar la intersección(s) de una ecuación, sustituto en x = 0 y resolver para y.

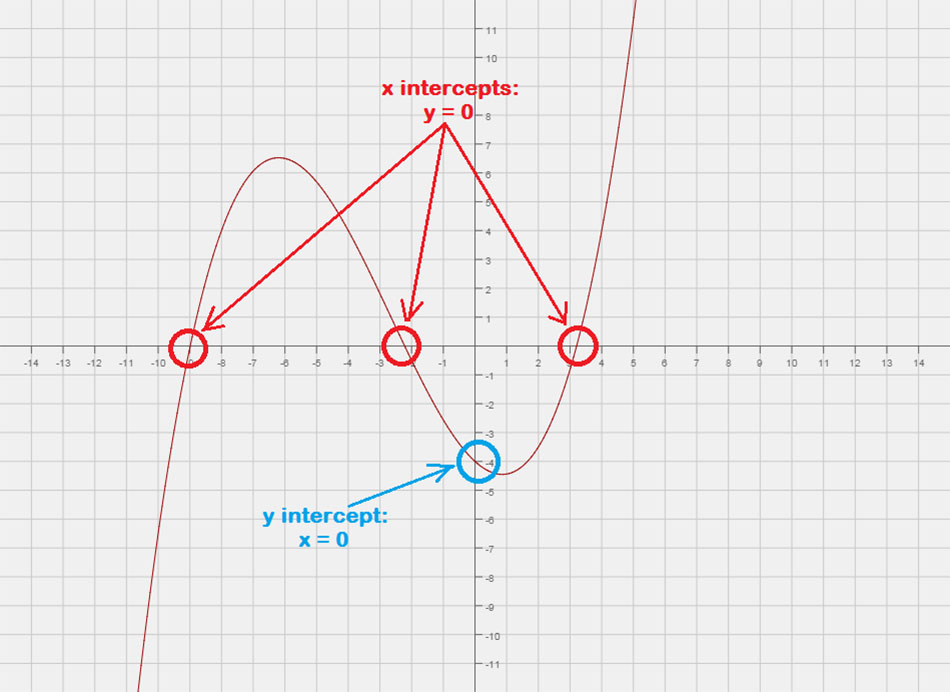
Las intercepciones X

los intersecciones x son puntos donde la gráfica de una función o una ecuación cruza o "toca" el eje x del plano cartesiano. Puede pensar en esto como un punto con valor de y de cero.

• Para encontrar las intersecciones con el eje x de una ecuación, dejar $y=0$ entonces resuelve para $X$.
• En una notación de puntos, está escrito como \izquierda( {X,0} \Correcto)(X,0).

Intersección x de una función lineal o una Derecho Línea

intersecciones con el eje x de una cuadrática Función o parábola

Las intersecciones en Y

los intersecciones y son puntos donde la gráfica de una función o una ecuación cruza o "toca" el eje y del plano cartesiano. Puede pensar en esto como un punto con valor x de cero.

• Para encontrar las intersecciones y de una ecuación, dejar $X=0$ entonces resuelve para $y$.
• En una notación de puntos, está escrito como \izquierda( {0,y} \Correcto)(0,y).

Intersección y de una función lineal o una línea recta

Intersección en y de una función cuadrática o parábola

Ejemplos de cómo encontrar las intersecciones en x e y de una línea, Parábola, y círculo

Ejemplo 1: Del gráfico, describir las intersecciones en xey usando notación de puntos.

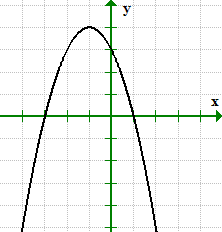
La gráfica cruza el eje x en X = 1 y X = 3, por lo tanto, podemos escribir las intersecciones con el eje x como puntos (1,0) y (–3, 0).

similar, el gráfico cruza el eje y en y = 3. Su intersección con el eje y se puede escribir como el punto (0,3).

Ejemplo 2: Encuentra las intersecciones en xey de la recta y = –2X + 4.

Para encontrar las intersecciones x algebraicamente, dejamos y = 0 en la ecuación y luego resuelva los valores de X. De la misma manera, encontrar las intersecciones en y algebraicamente, dejamos X = 0 en la ecuación y luego resuelve para y.

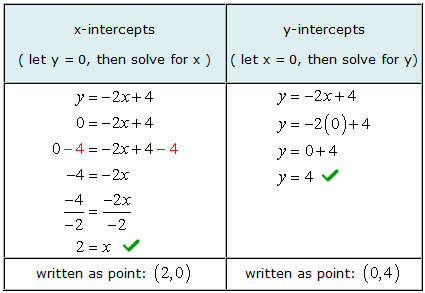
Aquí está el gráfico para verificar que nuestras respuestas sean correctas.

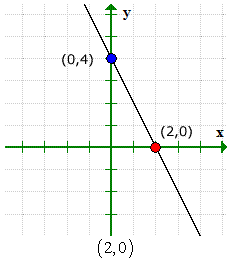
Ejemplo 3: Encuentra las intersecciones en x e y de la ecuación cuadrática y = X² - 2X - 3.

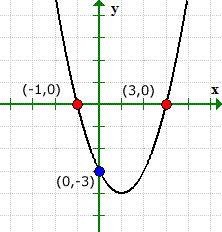
La gráfica de esta ecuación cuadrática es una parábola. Esperamos que tenga una forma de "U" donde se abriría hacia arriba o hacia abajo.

Para resolver la intersección con el eje x de este problema, Vas a factorizar un trinomio simple. Luego, estableces cada factor binomial igual a cero y resuelves para x.

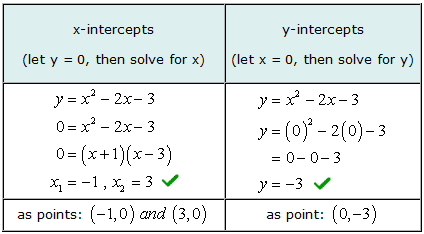
Nuestros valores resueltos para las intersecciones en x e y coinciden con la solución gráfica.

Ejemplo 4: Encuentra las intersecciones en x e y de la ecuación cuadrática y = 3X² + 1.

Este es un ejemplo donde la gráfica de la ecuación tiene una intersección con el eje y pero sin una intersección con el eje x.

• Busquemos la intersección con el eje y primero porque es extremadamente fácil! Enchufe x = 0 luego resuelve para y.

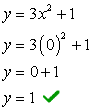
• Ahora para la intersección con el eje x. Enchufe y = 0, y resolver para x.

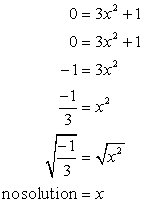
La raíz cuadrada de un número negativo es imaginaria. Esto sugiere que esta ecuación no tiene una intersección con el eje x!

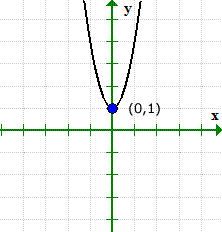
El gráfico puede verificar lo que está pasando. Observe que la gráfica cruzó el eje y en (0,1), pero nunca lo hice con el eje x.

Ejemplo 5: Encuentra las intersecciones en xey del círculo (X + 4)² + (y + 2)² = 8.

Este es un buen ejemplo para ilustrar que es posible que la gráfica de una ecuación tenga intersecciones x pero sin intersecciones y.

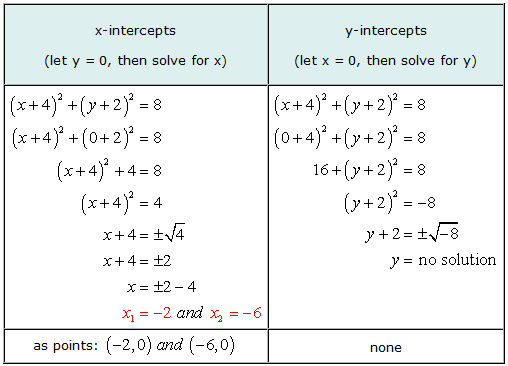
Al resolver para y, llegamos a la situación de intentar obtener la raíz cuadrada de un número negativo. La respuesta es imaginaria, por lo tanto, sin solución. Eso significa que la ecuación no tiene intersecciones y.

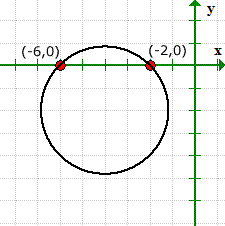
El gráfico verifica que estamos en lo correcto para los valores de nuestras intersecciones x, y no tiene intersecciones y.

Crédito:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/