¿Cuáles son los escenarios de la vida real que involucran ecuaciones cuadráticas??
Hay muchas situaciones reales que involucran cuadráticas y parábolas.. Lanzando una pelota, disparar un cañón, zambullirse desde una plataforma, y golpear una pelota de golf son ejemplos de situaciones que se pueden simular usando funciones cuadráticas.
La ecuación cuadrática se usa prácticamente en astronomía., matemáticas, Ingenieria, medicamento, financiar, silvicultura, ciencia o investigacion, etc.. En cualquier campo, si hay una actividad académica o investigadora, Es probable que exista un sistema de ecuaciones que requiera una ecuación cuadrática para resolver.
Para la vida ordinaria, sin el uso de ningún material académico, no se necesitan matemáticas o ecuaciones; y, por lo tanto, no se requiere una ecuación cuadrática.
Te sorprenderá la cantidad de aplicaciones que usan ecuaciones cuadráticas.
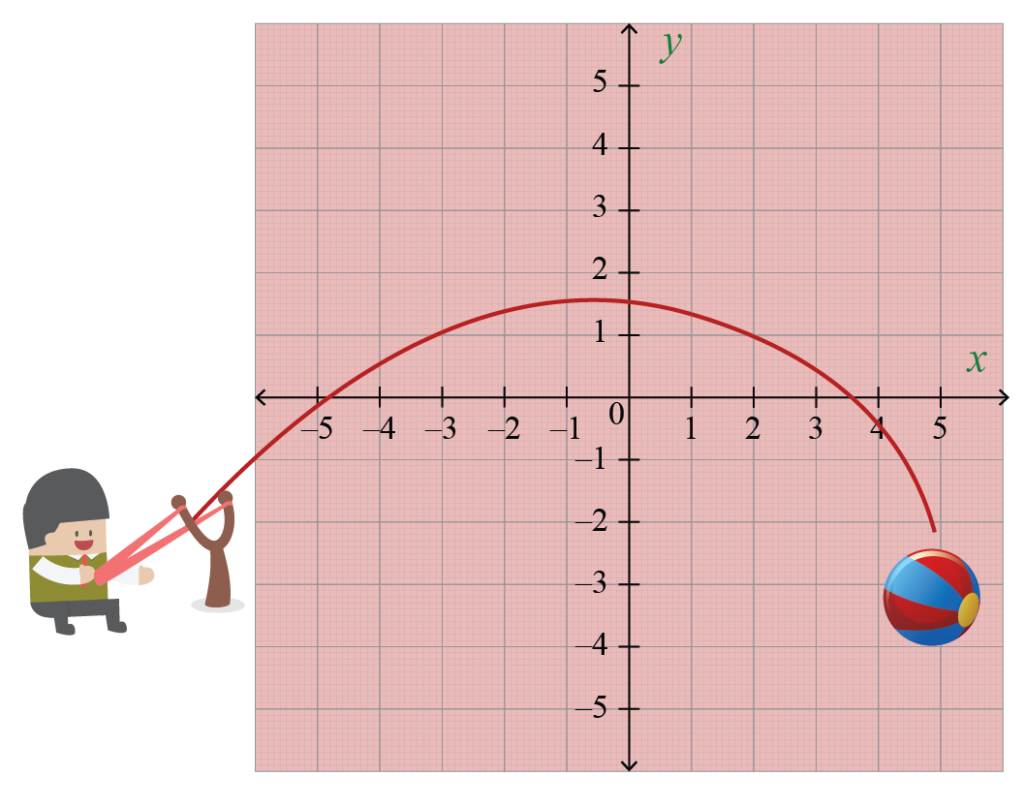
Lanzar una pelota al aire. El arco que sigue es una parábola.. Y una parábola se puede representar mediante una ecuación cuadrática.
¿Cuál es el foco de una parábola?? Una forma de definir una parábola es que es el conjunto de puntos en el plano equidistantes de una línea dada., llamado la directriz, y un punto dado, llamado el foco.
¿Cómo se aplican las ecuaciones cuadráticas en nuestra vida diaria??
Las ecuaciones cuadráticas se utilizan a menudo en la vida cotidiana.. La fuerza de la gravedad es proporcional al cuadrado inverso de la distancia a la Tierra., tan proyectiles, de una pelota de tenis a un cohete, volar a lo largo de una trayectoria parabólica.
Suponga que quiere revolver el café, la fuerza centrípeta del café es de naturaleza cuadrática, así que cuando quites la cuchara, te das cuenta de que tiene forma de paraboloide (imagina una parábola tridimensional).
Las ecuaciones cuadráticas se utilizan a menudo en problemas de optimización tanto en ingeniería como en finanzas., cuando desee minimizar el costo de un bien en particular o maximizar las ganancias, y a veces esto se puede modelar mediante ecuaciones cuadráticas (aunque no siempre).
La forma de determinar la resistencia de las resistencias en paralelo requiere una comprensión práctica de la resolución de ecuaciones cuadráticas, si conoces algunas conclusiones, por lo que es importante tener la combinación correcta de resistencias para no destruir elementos importantes del circuito.
Los espejos parabólicos y los micrófonos utilizan la misma característica de las parábolas y, por lo tanto, los paraboloides., que es que pueden concentrar reflejos en un punto, que da una muy buena imagen para un telescopio o una señal clara de un micrófono.
Ahora algunas aplicaciones todavía cotidianas, pero a mayor escala, están en EDO de segundo orden, que requieren una ecuación auxiliar para resolver, que es una ecuación cuadrática, y cuyo resultado determina la función para todo el sistema.
Ejemplos de usos de esta ecuación son oscilaciones que utilizan movimiento armónico simple, como los resortes en su automóvil o los resortes en la mayoría de los dispositivos mecánicos en el suelo.
Origen de la ecuación cuadrática
Los babilonios fueron los primeros en inventar ecuaciones cuadráticas desde el año 2000 a. C.. Los necesitaban para cálculos agrícolas y de riego..
Los griegos los usaron más tarde. – Arquímedes recurrió a ellos para encontrar el valor del radio de un círculo..
Hoy los usamos todos los días para calcular el área. (el tamaño de una caja, una sala de estar, una parcela de tierra), para determinar el beneficio de una mercancía (¿Cuánto de este producto necesito vender para obtener ganancias??) o para estimar la velocidad de un objeto (si te tiro algo – algo sólido, – ¿Cuánto tiempo tardará en que lo que tiro acabe en tus manos??)
Las razones para querer encontrar una solución a tales problemas no se conocen completamente., pero podemos hacer conjeturas.
Por ejemplo, Es posible que hayan tenido una cierta cantidad de material con el que encerrar un campo rectangular de un área determinada.. Quizás necesitaban saber cuál era la cantidad ideal de material a utilizar para ese perímetro., o si tuvieran suficiente.
Cualesquiera que sean sus necesidades, tenían una solución al problema. Lo escribieron paso a paso de la siguiente manera:
X + y =s; ………………………………………… (1)
xy=una; ……………………………………………. (2)
(1) Encuentra la mitad de s.
(2) Eleve al cuadrado el número obtenido en 1.
(3) Reste el número que se encuentra en 2 por una.
(4) Encuentra la raíz cuadrada del número que se encuentra en 3.
(5) Suma el número obtenido en 1 al número obtenido en 4. Esta es la longitud de uno de los lados.
Realización de paso 4 fue la parte mas dificil, aunque se sabe que los babilonios usaron mesas cuadradas, presumiblemente contiene una lista de números cuadrados, para aproximar la raíz cuadrada de un número.
Algunos historiadores también atribuyen a los babilonios la primera aplicación del método de Newton, que se usó específicamente para encontrar raíces cuadradas.
Lo interesante de todo esto es cómo la fórmula cuadrática (∗) surgió de tal problema. Después de todo, no estamos resolviendo una ecuación cuadrática aquí, pero un par de ecuaciones simultáneas (1) y (2).
Esto no es dificil de ver, usando las notaciones de hoy. De (1) obtenemos y = s-x, que cuando se sustituye en (2) da:
X(s-X)=una.
sX-X2=una.
X2-sX+una=0.
Así, (1) y (2) son equivalentes a resolver la ecuación cuadrática x2-sx + a = 0. Específicamente, esto nos dice que en esta ecuación cuadrática, el coeficiente de x es el negativo de la suma de las dos soluciones (ecuación (1) ), y el coeficiente de uno es el producto de las dos soluciones (ecuación (2) ).



Deja una respuesta
Debes iniciar sesión o registro para agregar una nueva respuesta.