Il est très simple d'identifier les x et y INTERCEPTIONS sur un graphique, mais les étudiants ont souvent du mal à les trouver en utilisant uniquement l'équation. toutefois, il faut juste un truc simple:

Pour trouver le point d'intersection x(s) d'une équation, en remplaçant y = 0 et résoudre pour x.

Pour trouver l'ordonnée(s) d'une équation, remplaçant en x = 0 et résoudre pour y.

Les X-Intercepts

le interceptions x sont des points où le graphique d'une fonction ou d'une équation croise ou «touche» l'axe des x du plan cartésien. Vous pouvez considérer cela comme un point avec une valeur y de zéro.

• Pour trouver les abscisses d'une équation, laisser $et=0$ puis résolvez pour $X$.
• Dans une notation ponctuelle, il s'écrit \la gauche( {X,0} \droite)(X,0).

X-intercept d'une fonction linéaire ou d'un Droit Ligne

X-interceptions d'un quadratique Une fonction ou parabole

Les interceptions en Y

le interceptions y sont des points où le graphique d'une fonction ou d'une équation croise ou «touche» l'axe y du plan cartésien. Vous pouvez considérer cela comme un point avec une valeur x de zéro.

• Pour trouver les ordonnées à l'origine d'une équation, laisser $X=0$ puis résolvez pour $et$.
• Dans une notation ponctuelle, il s'écrit \la gauche( {0,et} \droite)(0,et).

ordonnée à l'origine d'une fonction linéaire ou d'une ligne droite

ordonnée à l'origine d'une fonction quadratique ou d'une parabole

Exemples de recherche des interceptions x et y d'une ligne, Parabole, et cercle

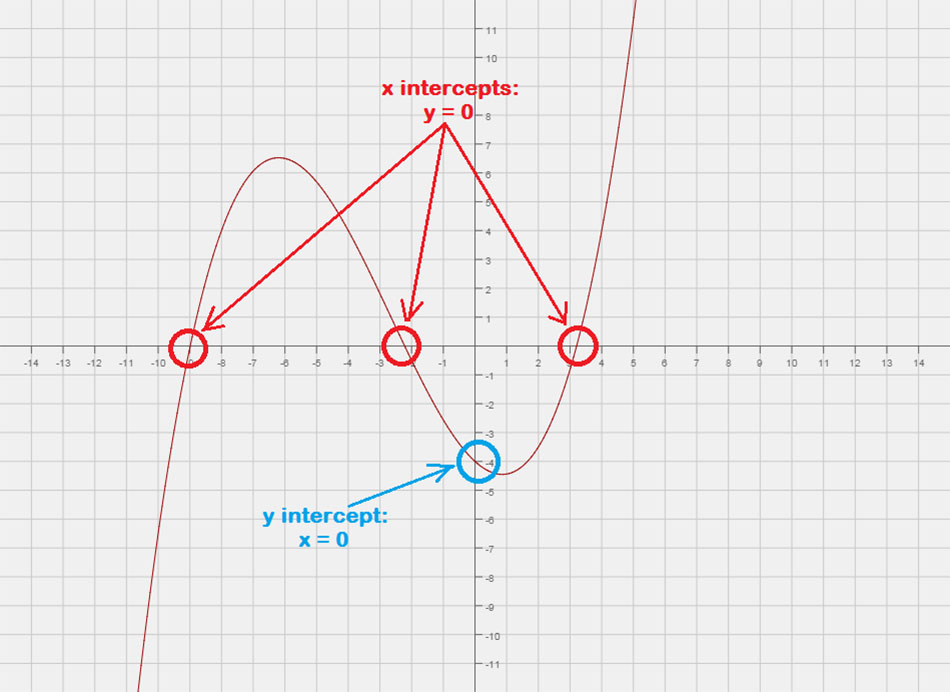
Exemple 1: À partir du graphique, décrire les abscisses x et y en utilisant la notation par points.

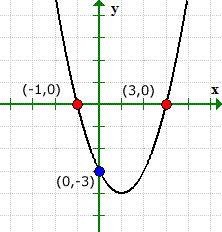
Le graphique croise l'axe des x à X = 1 et X = 3, donc, nous pouvons écrire les abscisses sous forme de points (1,0) et (–3, 0).

De même, le graphique croise l'axe y à et = 3. Son ordonnée à l'origine peut être écrite comme le point (0,3).

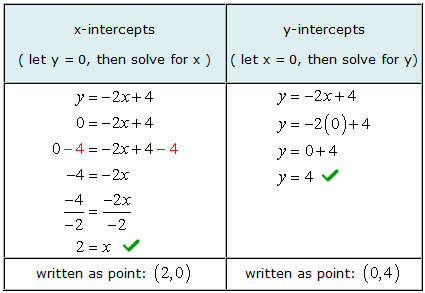
Exemple 2: Trouvez les abscisses x et y de la ligne et = –2X + 4.

Pour trouver les abscisses algébriques, on laisse et = 0 dans l'équation, puis résolvez les valeurs de X. De la même manière, rechercher algébriquement les ordonnées à l'origine, on laisse X = 0 dans l'équation, puis résolvez pour et.

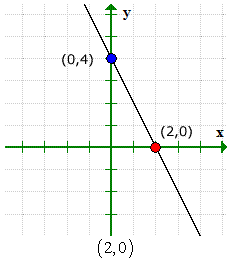
Voici le graphique pour vérifier que nos réponses sont correctes.

Exemple 3: Trouvez les abscisses x et y de l'équation quadratique et = X² - 2X - 3.

Le graphique de cette équation quadratique est une parabole. Nous nous attendons à ce qu'il ait une forme en «U» où il s'ouvrirait vers le haut ou vers le bas.

Pour résoudre l'ordonnée à l'origine de ce problème, vous serez factoriser un trinôme simple. Ensuite, vous définissez chaque facteur binomial égal à zéro et résolvez pour x.

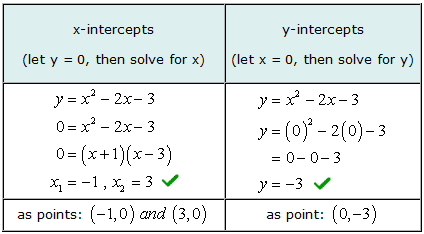
Nos valeurs résolues pour les interceptions x et y correspondent à la solution graphique.

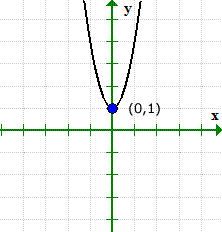
Exemple 4: Trouvez les abscisses x et y de l'équation quadratique et = 3X² + 1.

Ceci est un exemple où le graphe de l'équation a un ordonnée à l'origine mais sans une ordonnée à l'origine.

• Trouvons d'abord l'ordonnée à l'origine, car c'est extrêmement facile! Branchez x = 0 puis résolvez pour y.

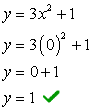
• Maintenant pour l'interception x. Branchez y = 0, et résoudre pour x.

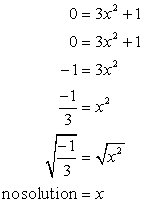
La racine carrée d'un nombre négatif est imaginaire. Cela suggère que cette équation n'a pas une interception x!

Le graphique peut vérifier ce qui se passe. Notez que le graphique a croisé l'axe des y à (0,1), mais jamais fait avec l'axe des x.

Exemple 5: Trouvez les interceptions x et y du cercle (X + 4)² + (et + 2)² = 8.

Ceci est un bon exemple pour illustrer qu'il est possible pour le graphique d'une équation d'avoir des abscisses à l'origine mais sans ordonnées à l'origine.

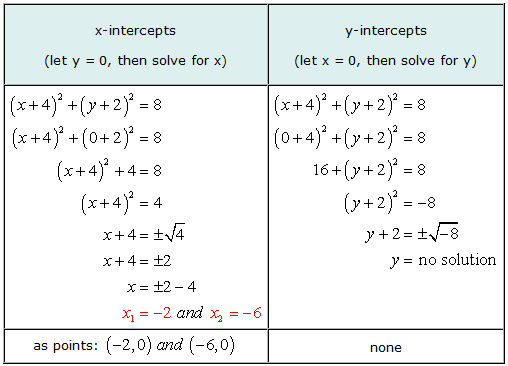
Lors de la résolution de y, nous sommes arrivés à la situation d'essayer d'obtenir la racine carrée d'un nombre négatif. La réponse est imaginaire, Ainsi, pas de solution. Cela signifie que l’équation n’a pas d’ordonnée à l'origine.

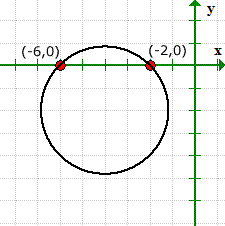
Le graphique vérifie que nous avons raison pour les valeurs de nos abscisses, et il n'a pas d'ordonnée à l'origine.

Crédit:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/