Come trovare le intercettazioni xe y di un'equazione
È molto semplice identificare le intercettazioni xey su un grafico, ma gli studenti spesso fanno fatica a trovarli usando solo l'equazione. tuttavia, richiede solo un semplice trucco:
Per trovare l'intercetta x(S) di un'equazione, sostituto in y = 0 e risolvi per x.
Per trovare l'intercetta y(S) di un'equazione, sostituire in x = 0 e risolvi per y.
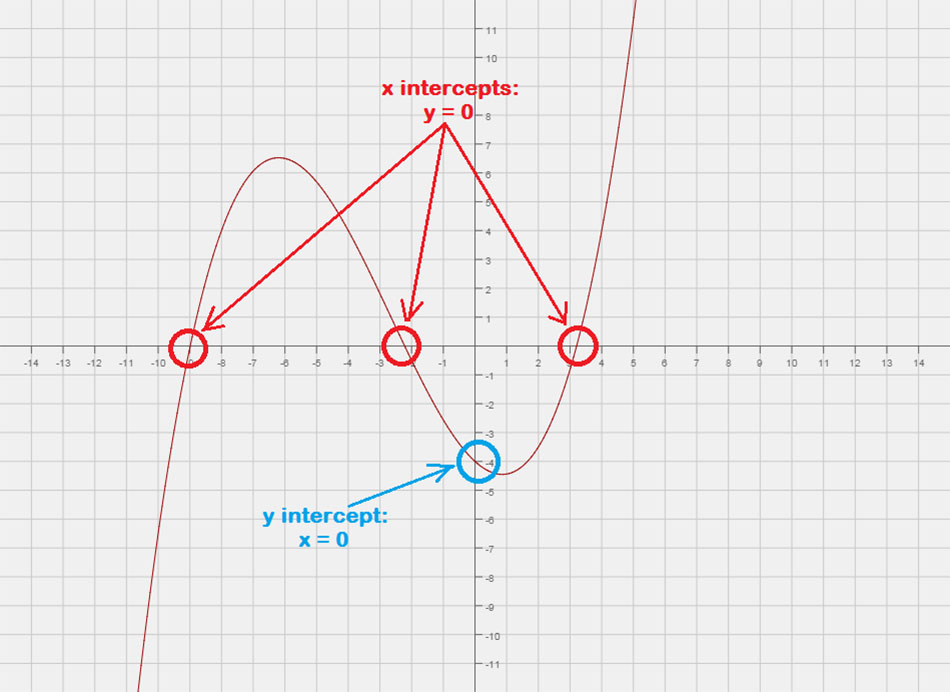
Le intercettazioni X.
Il x-intercetta sono punti in cui il grafico di una funzione o di un'equazione incrocia o “tocca” l'asse x del Piano Cartesiano. Puoi pensare a questo come a un punto con valore y pari a zero.
- Per trovare le intercettazioni x di un'equazione, permettere y = 0 allora risolvi per X.
- In una notazione puntuale, è scritto come \sinistra( {X,0} \destra).
intercetta x di una funzione lineare o a Dritto Linea

intercetta-x di un quadratico Funzione o Parabola

Le intercettazioni Y.
Il y-intercette sono punti in cui il grafico di una funzione o di un'equazione incrocia o “tocca” l'asse y del Piano Cartesiano. Puoi pensare a questo come a un punto con valore x pari a zero.
- Per trovare le intercettazioni y di un'equazione, permettere x = 0 allora risolvi per e.
- In una notazione puntuale, è scritto come \sinistra( {0,e} \destra).
intercetta y di una funzione lineare o di una linea retta

intercetta y di una funzione quadratica o parabola

Esempi di come trovare le intercettazioni xey di una linea, Parabola, e Cerchio
Esempio 1: Dal grafico, descrivere le intercettazioni xey utilizzando la notazione puntuale.
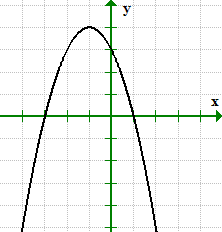
Il grafico attraversa l'asse x in X = 1 e X = 3, perciò, possiamo scrivere le intercettazioni x come punti (1,0) e (-3, 0).
allo stesso modo, il grafico attraversa l'asse y in e = 3. La sua intercetta y può essere scritta come punto (0,3).
Esempio 2: Trova le intercette x e y della retta e = –2X + 4.
Per trovare le intercettazioni x algebricamente, lasciamo e = 0 nell'equazione e quindi risolvere per i valori di X. Allo stesso modo, per trovare intercettazioni y algebricamente, lasciamo X = 0 nell'equazione e quindi risolvere per e.
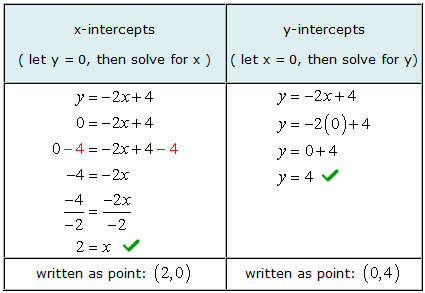
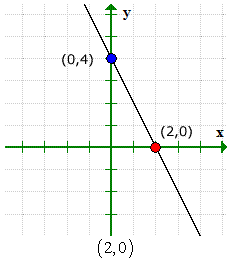
Ecco il grafico per verificare che le nostre risposte siano corrette.
Esempio 3: Trova le intercette x e y dell'equazione quadratica e = X2 - 2X - 3.
Il grafico di questa equazione quadratica è una parabola. Ci aspettiamo che abbia una forma a "U" dove si aprirà o si abbasserà.
Per risolvere l'intercetta x di questo problema, desideri fattore un trinomio semplice. Quindi imposta ogni fattore binomiale uguale a zero e risolvi per x.
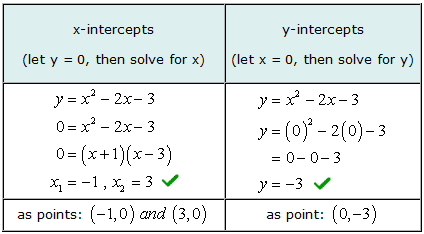
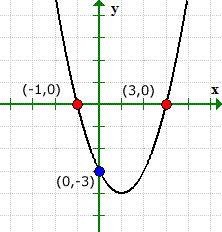
I nostri valori risolti per entrambe le intercettazioni x e y corrispondono alla soluzione grafica.
Esempio 4: Trova le intercette x e y dell'equazione quadratica e = 3X2 + 1.
Questo è un esempio in cui il grafico dell'equazione ha un'intercetta y ma senza un'intercetta x.
- Troviamo prima l'intercetta y perché è estremamente facile! Collega x = 0 quindi risolvi per y.
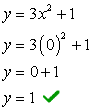
- Ora per l'intercetta x. Inserisci y = 0, e risolvi per x.
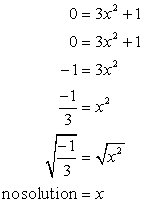
La radice quadrata di un numero negativo è immaginaria. Ciò suggerisce che questa equazione non ha un'intercetta x!
Il grafico può verificare cosa sta succedendo. Si noti che il grafico ha attraversato l'asse y in (0,1), ma non l'ho mai fatto con l'asse x.
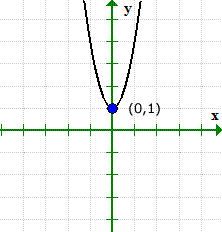
Esempio 5: Trova le intercette x e y del cerchio (X + 4)2 + (e + 2)2 = 8.
Questo è un buon esempio per illustrare che è possibile che il grafico di un'equazione abbia intercettazioni x ma senza intercettazioni y.
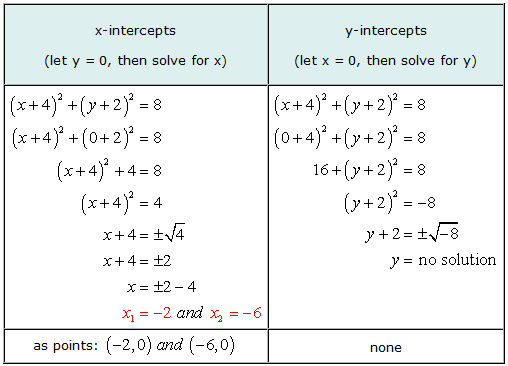
Nel risolvere per y, siamo arrivati alla situazione di cercare di ottenere la radice quadrata di un numero negativo. La risposta è immaginaria, così, nessuna soluzione. Ciò significa che l'equazione non ha alcuna intercettazione y.
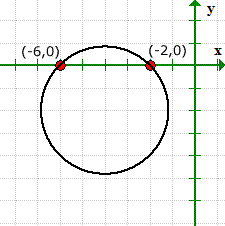
Il grafico verifica che siamo giusti per i valori delle nostre intercettazioni x, e non ha intercettazioni y.
Credito:
https://www.studiosity.com/blog/
https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/



Lascia una risposta
Devi accesso o Registrati per aggiungere una nuova risposta.