Quais são os cenários da vida real envolvendo equações quadráticas?
Existem muitas situações reais envolvendo quadráticas e parábolas. Jogando uma bola, atirando um canhão, mergulhando de uma plataforma, e acertar uma bola de golfe são exemplos de situações que podem ser simuladas usando funções quadráticas.
A equação quadrática é praticamente usada na astronomia, matemática, Engenharia, remédio, finança, silvicultura, ciência ou pesquisa, etc. Em qualquer campo, se há uma atividade acadêmica ou de pesquisa, é provável que haja um sistema de equações que pode exigir uma equação quadrática para resolver.
Para a vida normal, sem o uso de quaisquer materiais acadêmicos, matemática ou equações não são necessárias; e, assim sendo, uma equação quadrática não é necessária.
Você ficará surpreso com o número de aplicativos que usam equações quadráticas.
Jogue uma bola no ar. O arco que segue é uma parábola. E uma parábola pode ser representada por uma equação quadrática.
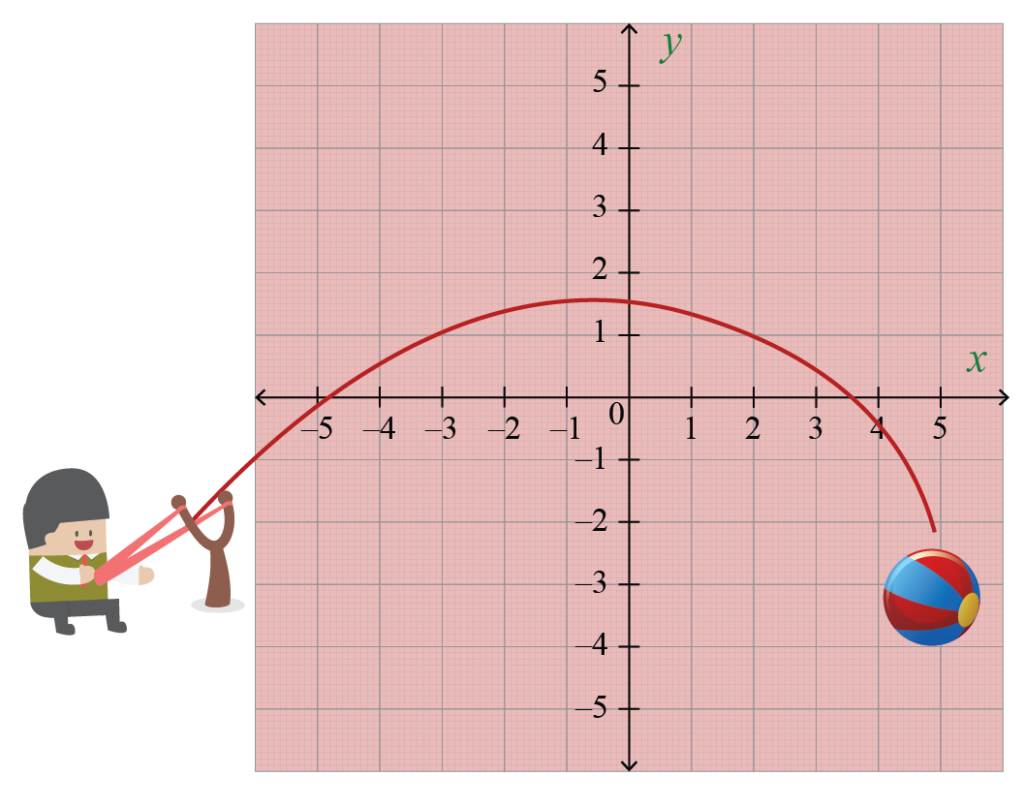
Qual é o foco de uma parábola? Uma maneira de definir uma parábola é que ela é o conjunto de pontos no plano equidistantes de uma dada linha, chamado de diretriz, e um determinado ponto, chamado de foco.
Como as equações quadráticas são aplicadas em nossa vida cotidiana?
Equações quadráticas são frequentemente usadas na vida cotidiana. A força da gravidade é proporcional ao inverso do quadrado da distância da Terra, tão projéteis, de uma bola de tênis a um foguete, voar ao longo de uma trajetória parabólica.
Suponha que você queira mexer o café, a força centrípeta do café é de natureza quadrática, então quando você remove a colher, você percebe que ele forma uma forma paraboloide (imagine uma parábola tridimensional).
As equações quadráticas são frequentemente usadas em problemas de otimização em engenharia e finanças, quando você deseja minimizar o custo de um determinado bem ou maximizar o lucro, e às vezes isso pode ser modelado por equações quadráticas (embora nem sempre).
A maneira de determinar a resistência dos resistores em paralelo requer uma compreensão prática da resolução de equações quadráticas, se você sabe algumas conclusões, por isso é importante ter a combinação certa de resistores para não destruir elementos importantes do circuito.
Espelhos e microfones parabólicos usam o mesmo recurso de parábolas e, portanto, parabolóides, que é que eles podem concentrar reflexões em um ponto, que dá uma imagem muito boa para um telescópio ou um sinal claro de um microfone.
Agora algumas aplicações ainda cotidianas, mas em maior escala, estão em EDOs de 2ª ordem, que requerem uma equação auxiliar para resolver, que é uma equação quadrática, e cujo resultado determina a função para todo o sistema.
Exemplos de usos desta equação são balanços que usam movimento harmônico simples, como as molas do seu carro ou as molas da maioria dos dispositivos mecânicos no chão.
Origem da equação quadrática
Os babilônios foram os primeiros a inventar equações quadráticas já em 2000 aC. Eles precisavam deles para cálculos agrícolas e de irrigação.
Os gregos os usaram mais tarde – Arquimedes recorreu a eles para encontrar o valor do raio de um círculo.
Hoje nós os usamos todos os dias para calcular a área (o tamanho de uma caixa, uma sala de estar, um pedaço de terra), determinar o lucro de uma mercadoria (quanto dessa mercadoria eu preciso vender para ter lucro?) ou para estimar a velocidade de um objeto (se eu jogar algo em você – algo sólido, – quanto tempo vai demorar para o que eu jogo acabar em suas mãos?)
As razões para querer encontrar uma solução para tais problemas não são totalmente conhecidas, mas podemos fazer suposições.
Por exemplo, eles podem ter tido uma certa quantidade de material com o qual encerrar um campo retangular de uma determinada área. Talvez eles precisassem saber qual era a quantidade ideal de material a ser usado para esse perímetro, ou se eles tivessem o suficiente.
Quaisquer que sejam suas necessidades, eles tinham uma solução para o problema. Eles escreveram passo a passo da seguinte forma:
X + e =s; ………………………………………… (1)
xy=uma; ……………………………………………. (2)
(1) Encontre metade de s.
(2) Quadrado o número obtido em 1.
(3) Subtraia o número encontrado em 2 por uma.
(4) Encontre a raiz quadrada do número encontrado em 3.
(5) Adicione o número obtido em 1 ao número obtido em 4. Este é o comprimento de um dos lados.
Etapa de execução 4 foi a parte mais difícil, embora os babilônios sejam conhecidos por terem usado mesas quadradas, presumivelmente contendo uma lista de números quadrados, para aproximar a raiz quadrada de um número.
Alguns historiadores também atribuem aos babilônios a primeira aplicação do método de Newton, que foi usado especificamente para encontrar raízes quadradas.
O interessante sobre tudo isso é como a fórmula quadrática (∗) surgiu de tal problema. Depois de tudo, não estamos resolvendo uma equação quadrática aqui, mas um par de equações simultâneas (1) e (2).
Isso não é difícil de ver, usando as notações de hoje. A partir de (1) obtemos y = s-x, que quando substituído em (2) dá:
X(s-X)=uma.
sX-X2=uma.
X2-sX+uma=0.
portanto, (1) e (2) são equivalentes a resolver a equação quadrática x2-sx + a = 0. Especificamente, isso nos diz que nesta equação quadrática, o coeficiente de x é o negativo da soma das duas soluções (equação (1) ), e o coeficiente de um é o produto das duas soluções (equação (2) ).



Deixe uma resposta
Você deve Conecte-se ou registro para adicionar uma nova resposta.