这很简单，以确定在图表上的x和截距, 但学生经常使用奋斗仅方程找到他们. 然而, 它只是需要一个简单的技巧:

为了找到X轴截距(小号) 方程的, 替代在Y = 0 并求解X.

为了找到y轴截距(小号) 方程的, 替代在X = 0 解决y的.

X截距

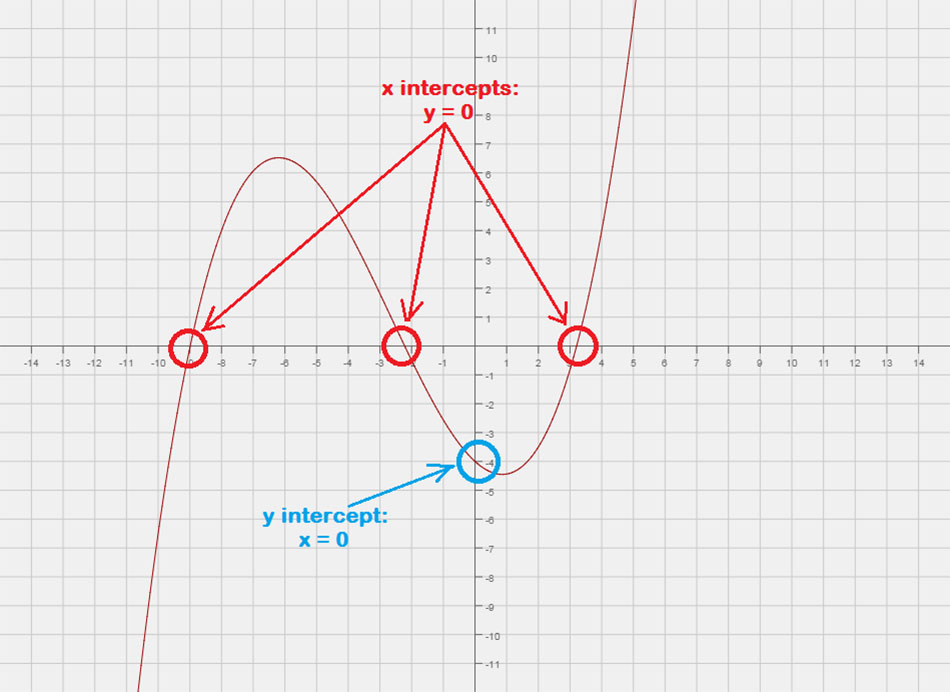
该 X截距 是函数或方程式的图形与笛卡尔平面的x轴交叉或“接触”的点. 您可能会认为这是y值为零的点.

• 查找方程的x截距, 让 $和=0$ 然后解决 $X$.
• 用点表示法, 它写为 \剩下( {X,0} \对)(X,0).

线性函数或a的x截距 直的 线

二次方的x截距 功能 或抛物线

Y轴截距

该 y截距 是函数或方程的图形与笛卡尔平面的y轴交叉或“接触”的点. 您可能会认为这是x值为零的点.

• 查找方程的y截距, 让 $X=0$ 然后解决 $和$.
• 用点表示法, 它写为 \剩下( {0,和} \对)(0,和).

线性函数或直线的y截距

二次函数或抛物线的y截距

如何找到一条线的x和y截距的示例, 抛物线, 和圆

例 1: 从图中, 使用点符号描述x和y截距.

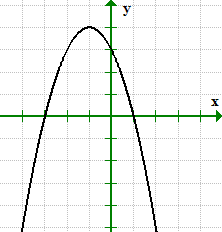
该图形与x轴交叉 X = 1 和 X = 3, 因此, 我们可以将x截距写为点 (1,0) 和 (–3, 0).

同样, 该图形与y轴交叉 和 = 3. 它的y截距可以写为一点 (0,3).

例 2: 找到直线的x和y截距 和 = –2X + 4.

以代数查找x截距, 我们让 和 = 0 在等式中，然后求解 X. 以相同的方式, 查找代数的y截距, 我们让 X = 0 在等式中，然后求解 和.

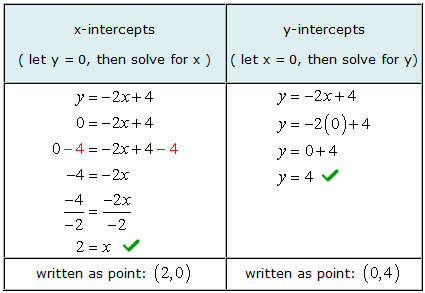
这是用来验证我们的答案正确的图表.

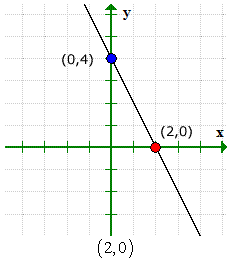
例 3: 找出二次方程的x和y截距 和 = X² - 2X - 3.

这个二次方程的图形是一个抛物线. 我们希望它具有“ U”形，可以向上或向下打开.

解决这个问题的X轴截距, 你会 分解一个简单的三项式. 然后，将每个二项式因子设置为零，并求解x.

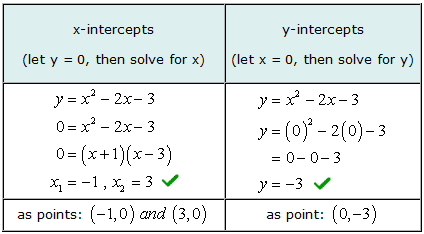
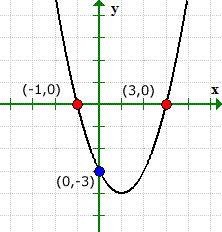
我们为x和y截距求解的值与图形解决方案相匹配.

例 4: 找出二次方程的x和y截距 和 = 3X² + 1.

这是一个示例，其中方程的图形具有y截距但没有x截距.

• 让我们先找到y截距，因为它非常容易! 插入x = 0 然后解y.

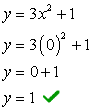
• 现在进行x截距. 插入y = 0, 并求解X.

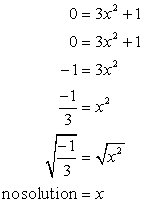
负数的平方根是虚数. 这表明这个等式 不具有 X截距!

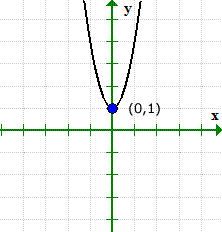
该图可以验证发生了什么. 请注意，图形在y轴上与y轴交叉 (0,1), 但从未在x轴上做过.

例 5: 找到圆的x和y截距 (X + 4)² + (和 + 2)² = 8.

这是一个很好的例子，可以说明方程的图形可能具有x截距但没有y截距.

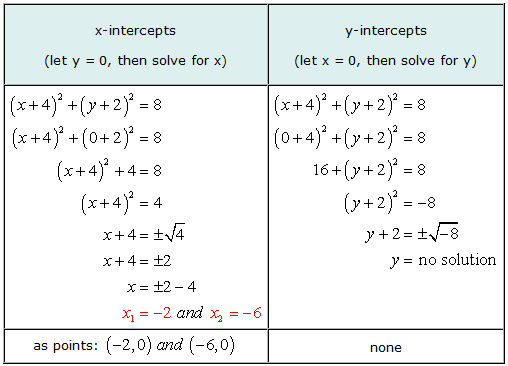
当求解y时, 我们得出了试图获得负数的平方根的情况. 答案是虚构的, 从而, 没有解决方案. 这意味着方程式没有任何y截距.

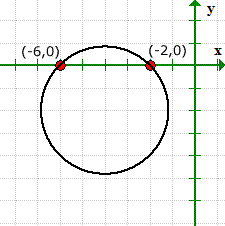
该图证明我们正确使用了x截距的值, 而且没有y截距.

信用:

HTTPS://www.studiosity.com/blog/

HTTPS://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/