什么是涉及二次方程的现实生活场景?
有很多涉及二次曲线和抛物线的真实情况. 扔球, 射击大炮, 跳下平台, 和击打高尔夫球都是可以使用二次函数模拟的情况的例子.
二次方程在天文学中的实际应用, 数学, 工程, 医学, 金融, 林业, 科学或研究, 等等. 在任何领域, 如果有学术或研究活动, 可能有一个方程组可能需要二次方程来求解.
为平凡的生活, 不使用任何学术材料, 不需要数学或方程式; 和, 因此, 不需要二次方程.
您会对使用二次方程的应用程序数量感到惊讶.
向空中扔一个球. 它所遵循的弧线是一条抛物线. 抛物线可以用二次方程表示.
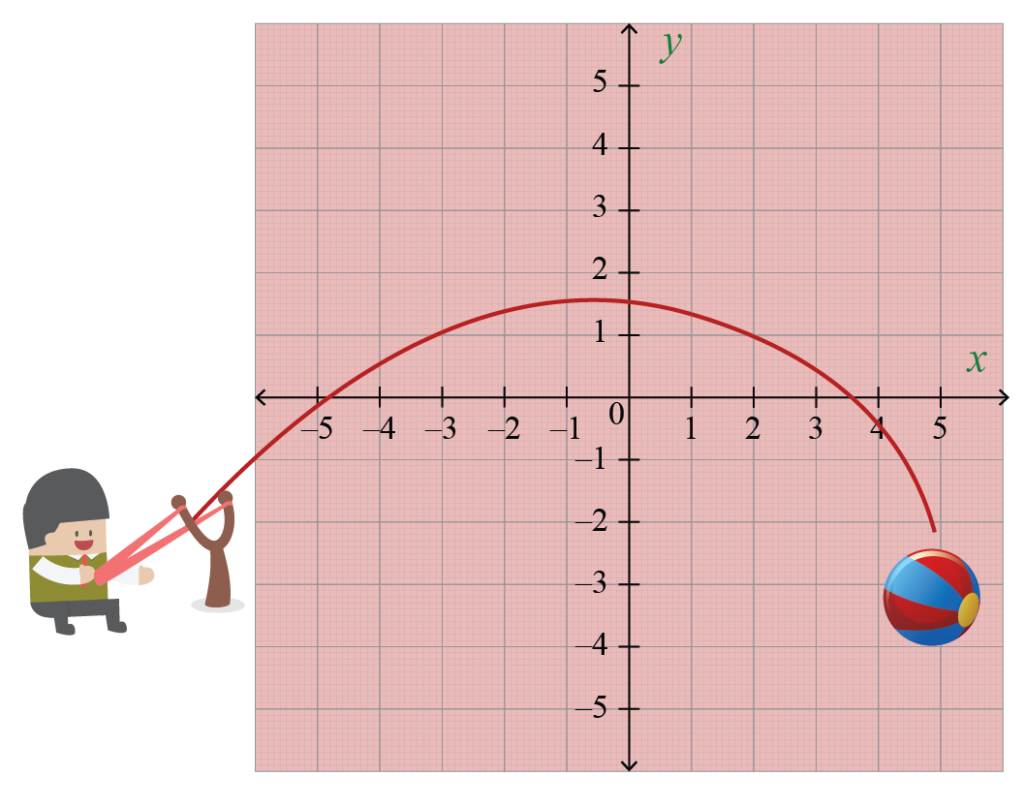
抛物线的焦点是什么? 定义抛物线的一种方法是它是平面中与给定直线等距的点集, 称为准线, 和一个给定的点, 叫焦点.
二次方程如何应用在我们的日常生活中?
日常生活中经常会用到二次方程. 重力与地球距离的平方成反比, 所以弹丸, 从网球到火箭, 沿抛物线轨迹飞行.
假设你想搅拌咖啡, 咖啡的向心力本质上是二次的, 所以当你取下勺子时, 你意识到它形成了一个抛物面形状 (想象一个三维抛物线).
二次方程常用于工程和金融中的优化问题, 当您想最小化特定商品的成本或最大化利润时, 有时这可以通过二次方程建模 (虽然不总是).
确定并联电阻的电阻的方法需要对求解二次方程有工作理解, 如果你知道一些结论, 所以重要的是要有正确的电阻组合,以免损坏重要的电路元件.
抛物面镜和麦克风使用抛物线的相同特征,因此也使用抛物面, 这是他们可以将反射集中在一点, 这为望远镜提供了非常好的图像或来自麦克风的清晰信号.
现在一些仍然是日常应用, 但在更大的范围内, 在二阶 ODE 中, 需要一个辅助方程来求解, 这是一个二次方程, 其结果决定了整个系统的功能.
该方程的使用示例是使用简谐运动的摆动, 就像汽车中的弹簧或地面上大多数机械设备中的弹簧.
二次方程的起源
早在公元前 2000 年,巴比伦人是第一个发明二次方程的人. 他们需要它们进行农业和灌溉计算.
希腊人后来使用了它们 – 阿基米德求助于他们来求圆半径的值.
今天我们每天都用它们来计算面积 (一个盒子的大小, 客厅, 一块地), 确定商品的利润 (我需要出售多少这种商品才能获利?) 或估计物体的速度 (如果我向你扔东西 – 坚固的东西, – 我扔的东西到你手里要多久?)
想要找到解决此类问题的方法的原因尚不完全清楚, 但我们可以猜测.
例如, 他们可能有一定数量的材料来包围给定区域的矩形区域. 也许他们需要知道用于该周边的理想材料量是多少, 或者如果他们有足够的.
无论他们需要什么, 他们确实有解决问题的办法. 他们是这样一步一步写下来的:
X + 和 =小号; ………………………………………… (1)
xy=一个; ……………………………………………. (2)
(1) 找到一半 小号.
(2) 平方得到的数字 1.
(3) 减去找到的数字 2 通过 一个.
(4) 找到在中找到的数字的平方根 3.
(5) 将中获得的数字相加 1 到4中得到的数字,这是其中一条边的长度.
执行步骤 4 是最难的部分, 虽然众所周知,巴比伦人使用方桌, 大概包含一个平方数列表, 逼近一个数的平方根.
一些历史学家还将牛顿方法的第一次应用归功于巴比伦人, 专门用于求平方根.
关于这一切的有趣之处在于二次公式如何 (*) 产生于这样的问题. 毕竟, 我们不是在这里求解二次方程, 但一对联立方程 (1) 和 (2).
这不难看出, 使用今天的符号. 从 (1) 我们得到 y=s-x, 当替换成 (2) 给:
X(小号 - X)=一个.
小号X - X2=一个.
X2 - 小号X+一个=0.
从而, (1) 和 (2) 等价于解二次方程 x2-sx+a=0. 特别, 这告诉我们在这个二次方程中, x 的系数是两个解之和的负数 (方程 (1) ), 并且一的系数是两个解的乘积 (方程 (2) ).



离开一个答案
你必须 登录 要么 寄存器 添加新答案.