Wat zijn de echte scenario's met kwadratische vergelijkingen??
Er zijn veel echte situaties met kwadraten en parabolen. Een bal gooien, een kanon schieten, van een platform duiken, en het slaan van een golfbal zijn allemaal voorbeelden van situaties die kunnen worden gesimuleerd met behulp van kwadratische functies.
De kwadratische vergelijking wordt praktisch gebruikt in de astronomie, wiskunde, bouwkunde, medicijn, financiën, bosbouw, wetenschap of onderzoek, enz. In elk veld, als er een academische of onderzoeksactiviteit is, er is waarschijnlijk een systeem van vergelijkingen waarvoor een kwadratische vergelijking nodig is om op te lossen.
Voor het gewone leven, zonder het gebruik van academisch materiaal, wiskunde of vergelijkingen zijn niet nodig; en, daarom, een kwadratische vergelijking is niet vereist.
U zult verrast zijn door het aantal toepassingen dat kwadratische vergelijkingen gebruikt.
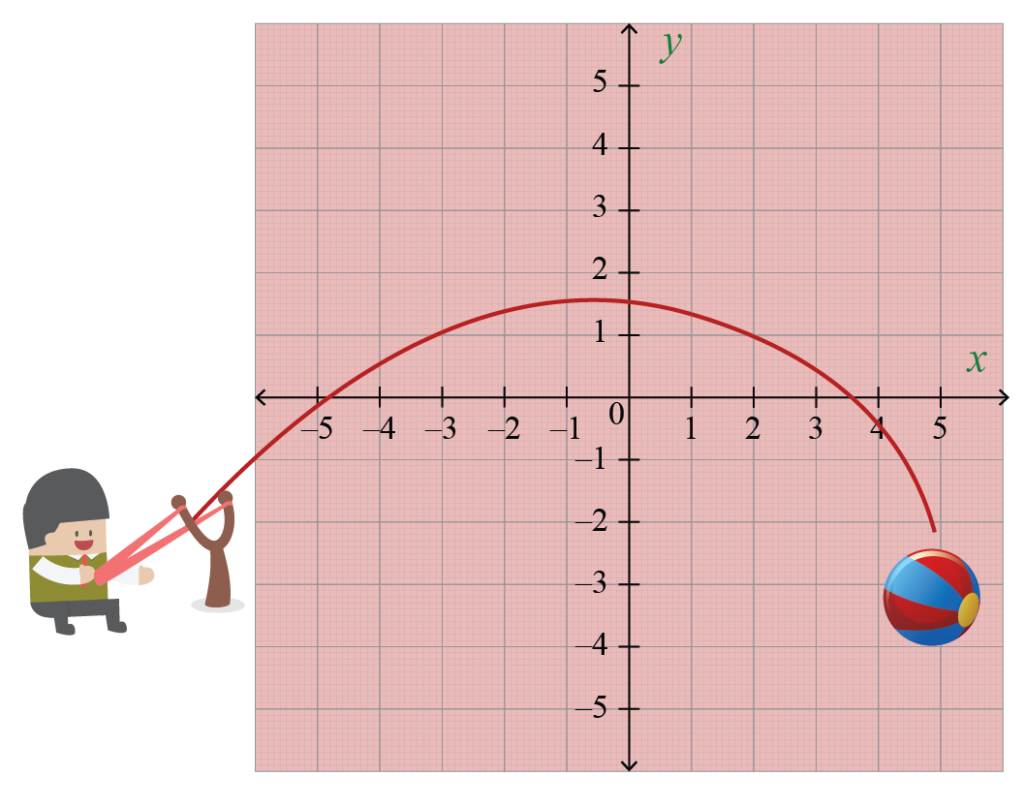
Gooi een bal in de lucht. De boog die volgt is een parabool. En een parabool kan worden weergegeven door een kwadratische vergelijking.
Wat is de focus van een parabool?? Een manier om een parabool te definiëren is dat het de verzameling punten is in het vlak op gelijke afstand van een gegeven lijn, de richtlijn genoemd, en een gegeven punt, de focus genoemd.
Hoe worden kwadratische vergelijkingen toegepast in ons dagelijks leven?
Kwadratische vergelijkingen worden vaak gebruikt in het dagelijks leven. De zwaartekracht is evenredig met het inverse kwadraat van de afstand tot de aarde, dus projectielen, van een tennisbal tot een raket, vliegen langs een parabolische baan.
Stel dat je koffie wilt roeren, de middelpuntzoekende kracht van koffie is kwadratisch van aard, dus als je de lepel verwijdert, je realiseert je dat het een paraboloïde vorm vormt (stel je een driedimensionale parabool voor).
Kwadratische vergelijkingen worden vaak gebruikt bij optimalisatieproblemen in zowel engineering als financiën, wanneer u de kosten van een bepaald goed wilt minimaliseren of de winst wilt maximaliseren, en soms kan dit worden gemodelleerd door kwadratische vergelijkingen (hoewel niet altijd).
De manier om de weerstand van de weerstanden parallel te bepalen, vereist een goed begrip van het oplossen van kwadratische vergelijkingen, als je wat conclusies weet, dus het is belangrijk om de juiste combinatie van weerstanden te hebben om belangrijke circuitelementen niet te vernietigen.
Parabolische spiegels en microfoons gebruiken dezelfde eigenschap van parabolen en dus paraboloïden, dat is dat ze reflecties op één punt kunnen concentreren, wat een zeer goed beeld geeft voor een telescoop of een helder signaal van een microfoon.
Nu nog wat alledaagse toepassingen, maar op grotere schaal, zijn in 2e orde ODE's, waarvoor een hulpvergelijking nodig is om op te lossen, wat een kwadratische vergelijking is, en waarvan het resultaat de functie voor het hele systeem bepaalt.
Voorbeelden van toepassingen van deze vergelijking zijn schommelingen die gebruik maken van eenvoudige harmonische beweging, zoals de veren in uw auto of de veren in de meeste mechanische apparaten op de grond.
Oorsprong van kwadratische vergelijking
De Babyloniërs waren de eersten die kwadratische vergelijkingen uitvonden, al in 2000 voor Christus. Ze hadden ze nodig voor landbouw- en irrigatieberekeningen.
De Grieken gebruikten ze later – Archimedes nam zijn toevlucht tot hen om de waarde van de straal van een cirkel te vinden.
Tegenwoordig gebruiken we ze elke dag om de oppervlakte te berekenen (de grootte van een doos, een woonkamer, Een stuk grond), om de winst van een goed te bepalen (hoeveel van deze grondstof moet ik verkopen om winst te maken??) of om de snelheid van een object te schatten (als ik iets naar je gooi – iets solides, – hoe lang duurt het voordat wat ik gooi in jouw handen terecht komt??)
De redenen om een oplossing voor dergelijke problemen te willen vinden, zijn niet volledig bekend, maar we kunnen raden.
Bijvoorbeeld, ze kunnen een bepaalde hoeveelheid materiaal hebben gehad om een rechthoekig veld van een bepaald gebied te omsluiten. Misschien moesten ze weten wat de ideale hoeveelheid materiaal was om voor die omtrek te gebruiken, of als ze genoeg hadden?.
Wat hun behoeften ook zijn, ze hadden wel een oplossing voor het probleem. Ze schreven het stap voor stap als volgt op::
X + en =s; ………………………………………… (1)
xy=een; ……………………………………………. (2)
(1) Vind de helft van s.
(2) Kwadraat van het verkregen getal in 1.
(3) Trek het gevonden getal af in 2 door een.
(4) Vind de vierkantswortel van het getal gevonden in 3.
(5) Voeg het verkregen nummer toe in 1 tot het getal verkregen in 4. Dit is de lengte van een van de zijden.
Stap uitvoeren: 4 was het moeilijkste deel, hoewel bekend is dat de Babyloniërs vierkante tafels hebben gebruikt, vermoedelijk met een lijst van vierkante getallen, om de vierkantswortel van een getal te benaderen.
Sommige historici schrijven de Babyloniërs ook de allereerste toepassing van Newtons methode toe, die specifiek werd gebruikt om vierkantswortels te vinden.
Het interessante van dit alles is hoe de kwadratische formule (∗) voortgekomen uit een dergelijk probleem. Ten slotte, we lossen hier geen kwadratische vergelijking op, maar een paar gelijktijdige vergelijkingen (1) en (2).
Dit is niet moeilijk te zien, de notaties van vandaag gebruiken. Van (1) we krijgen y=s-x, die wanneer vervangen in (2) geeft:
X(s-X)=een.
sX-X2=een.
X2-sX+een=0.
Dus, (1) en (2) zijn gelijk aan het oplossen van de kwadratische vergelijking x2-sx+a=0. specifiek, dit vertelt ons dat in deze kwadratische vergelijking, de coëfficiënt van x is de min van de som van de twee oplossingen (ln kan worden geschreven als = 1/x, terwijl log kan worden geschreven als = x of = xlog (1) ), en de coëfficiënt van één is het product van de twee oplossingen (ln kan worden geschreven als = 1/x, terwijl log kan worden geschreven als = x of = xlog (2) ).



Laat een antwoord achter
Je moet Log in of registreren om een nieuw antwoord toe te voegen.