É muito simples para identificar os X e Y interceptações em um gráfico, mas os estudantes frequentemente lutam para encontrá-los usando apenas a equação. Contudo, requer apenas um truque simples:

Para encontrar o x interceptar(s) de uma equação, substituto em y = 0 e resolver para x.

Para encontrar o y interceptar(s) de uma equação, substituto em x = 0 e resolver para y.

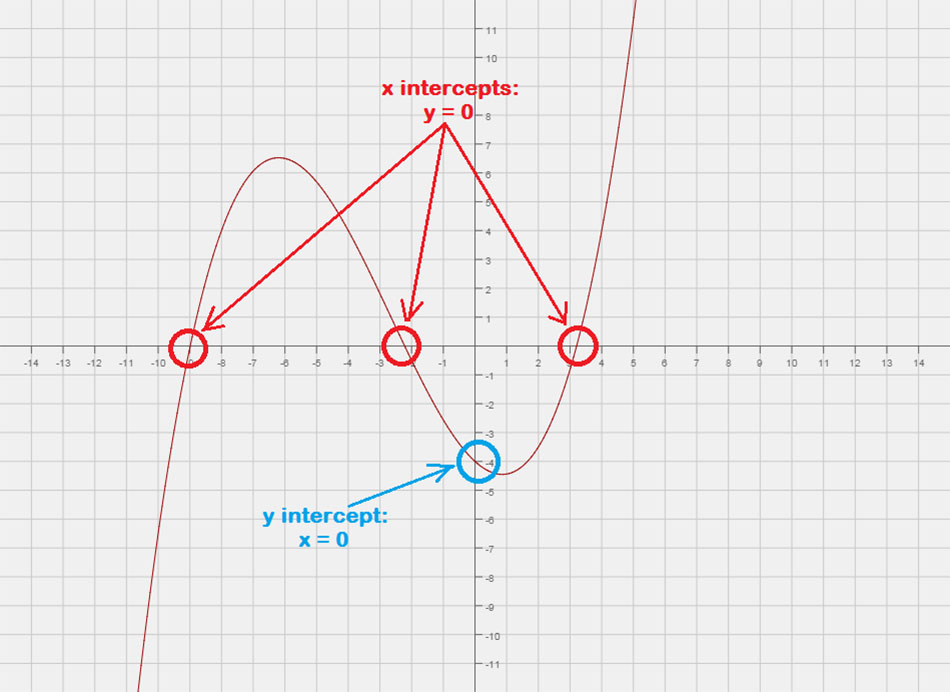
The X-Intercepts

o x-intercepta são pontos onde o gráfico de uma função ou equação cruza ou "toca" o eixo x do plano cartesiano. Você pode pensar nisso como um ponto com valor y de zero.

• Para encontrar os interceptos x de uma equação, deixar $e=0$ então resolva para $X$.
• Em uma notação de ponto, está escrito como \esquerda( {X,0} \certo)(X,0).

interceptação x de uma função linear ou um Direto Linha

interceptações x de um quadrático Função ou parábola

The Y-Intercepts

o interceptações y são pontos onde o gráfico de uma função ou equação cruza ou "toca" o eixo y do plano cartesiano. Você pode pensar nisso como um ponto com valor x de zero.

• Para encontrar os interceptos y de uma equação, deixar $X=0$ então resolva para $e$.
• Em uma notação de ponto, está escrito como \esquerda( {0,e} \certo)(0,e).

interceptação y de uma função linear ou linha reta

interceptação y de uma função quadrática ou parábola

Exemplos de como encontrar as interceptações xey de uma linha, Parábola, e círculo

Exemplo 1: Do gráfico, descreva as interceptações xey usando notação de ponto.

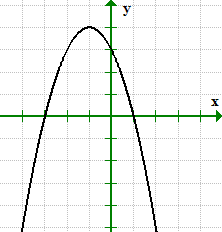
O gráfico cruza o eixo x em X = 1 e X = 3, assim sendo, podemos escrever as interceptações x como pontos (1,0) e (-3, 0).

similarmente, o gráfico cruza o eixo y em e = 3. Sua interceptação em y pode ser escrita como o ponto (0,3).

Exemplo 2: Encontre as interceptações xey da linha e = -2X + 4.

Para encontrar as interceptações x algebricamente, Nós deixamos e = 0 na equação e, em seguida, resolva os valores de X. Da mesma maneira, encontrar interceptações y algebricamente, Nós deixamos X = 0 na equação e, em seguida, resolva para e.

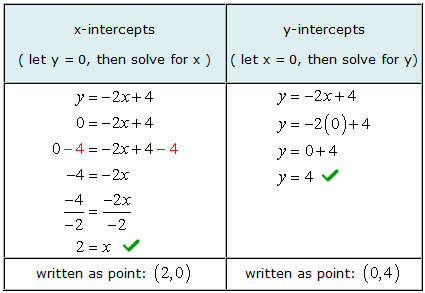
Aqui está o gráfico para verificar se nossas respostas estão corretas.

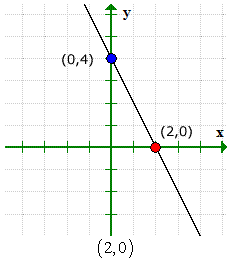
Exemplo 3: Encontre as interceptações xey da equação quadrática e = X² - 2X - 3.

O gráfico desta equação quadrática é uma parábola. Esperamos que tenha uma forma de “U” onde abriria para cima ou para baixo.

Para resolver a interceptação x deste problema, você irá fatorar um trinômio simples. Então você define cada fator binomial igual a zero e resolve para x.

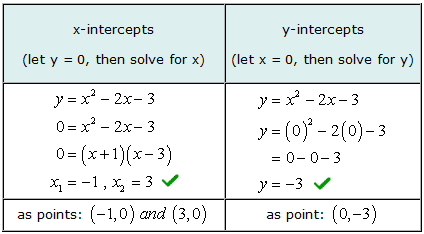
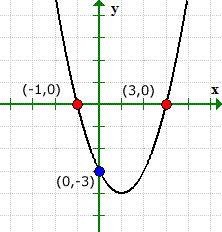
Nossos valores resolvidos para as interceptações xey coincidem com a solução gráfica.

Exemplo 4: Encontre as interceptações xey da equação quadrática e = 3X² + 1.

Este é um exemplo onde o gráfico da equação tem uma interceptação y, mas sem uma interceptação x.

• Vamos encontrar a interceptação y primeiro porque é extremamente fácil! Conecte x = 0 então resolva para y.

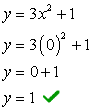
• Agora para a interceptação x. Conecte y = 0, e resolver para x.

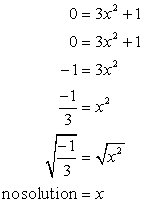
A raiz quadrada de um número negativo é imaginária. Isso sugere que esta equação não tem uma interceptação x!

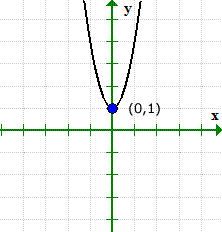
O gráfico pode verificar o que está acontecendo. Observe que o gráfico cruzou o eixo y em (0,1), mas nunca fez com o eixo x.

Exemplo 5: Encontre as interceptações xey do círculo (X + 4)² + (e + 2)² = 8.

Este é um bom exemplo para ilustrar que é possível para o gráfico de uma equação ter interceptos x, mas sem interceptos y.

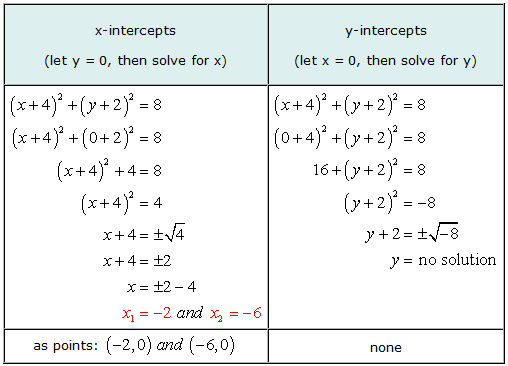
Ao resolver para y, chegamos à situação de tentar obter a raiz quadrada de um número negativo. A resposta é imaginária, portanto, nenhuma solução. Isso significa que a equação não tem interceptações y.

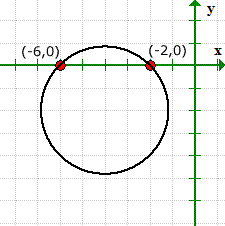
O gráfico verifica se estamos certos para os valores de nossas interceptações x, e não tem interceptações y.

Crédito:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/