الأمر في غاية البساطة لتحديد X و Y اعتراض على الرسم البياني, ولكن الطلاب النضال في كثير من الأحيان للعثور عليهم فقط باستخدام المعادلة. ومع ذلك, فإنه يتطلب مجرد خدعة بسيطة:

للعثور على س اعتراض(الصورة) معادلة, بديل في ص = 0 وحل ل x.

للعثور على اعتراض ذ(الصورة) معادلة, بديل في العاشر = 0 وحل لذ.

اعتراضات X

ال x- اعتراضات هي نقاط يتقاطع فيها الرسم البياني لدالة أو معادلة أو "يلامس" المحور السيني للمستوى الديكارتي. قد تفكر في هذا كنقطة ذات قيمة y تساوي صفرًا.

• لإيجاد تقاطع x لمعادلة, يترك $و=0$ ثم حل ل $س$.
• في تدوين نقطة, هو مكتوب على شكل \اليسار( {س,0} \حق)(س,0).

تقاطع x لوظيفة خطية أو أ مستقيم خط

تقاطع x من التربيعي وظيفة أو القطع المكافئ

اعتراضات ص

ال اعتراضات ص هي نقاط يتقاطع فيها الرسم البياني لدالة أو معادلة أو "يلامس" المحور الصادي للمستوى الديكارتي. قد تفكر في هذا على أنه نقطة بقيمة x تساوي صفرًا.

• لإيجاد تقاطع y للمعادلة, يترك $س=0$ ثم حل ل $و$.
• في تدوين نقطة, هو مكتوب على شكل \اليسار( {0,و} \حق)(0,و).

تقاطع ص لدالة خطية أو خط مستقيم

تقاطع ص لدالة تربيعية أو قطع مكافئ

أمثلة على كيفية إيجاد تقاطع x و y لخط, القطع المكافئ, ودائرة

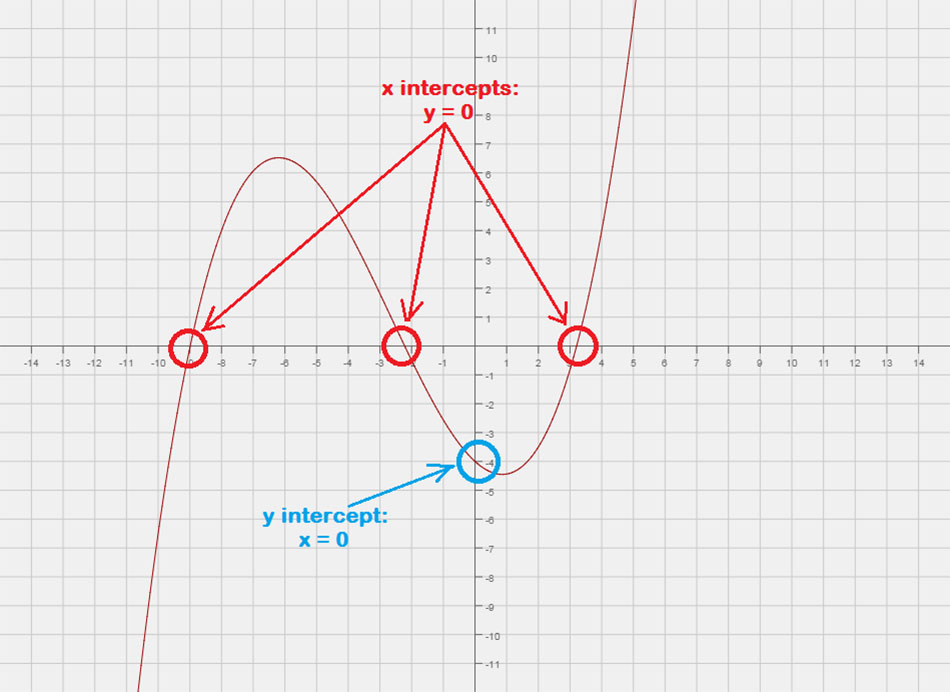
مثال 1: من الرسم البياني, صف تقاطع x و y باستخدام تدوين النقطة.

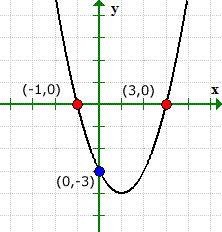
يقطع الرسم البياني المحور x عند س = 1 و س = 3, وبالتالي, يمكننا كتابة تقاطعات x كنقاط (1,0) و (–3, 0).

وبالمثل, يتقاطع الرسم البياني مع المحور ص عند و = 3. يمكن كتابة الجزء المقطوع من المحور y كنقطة (0,3).

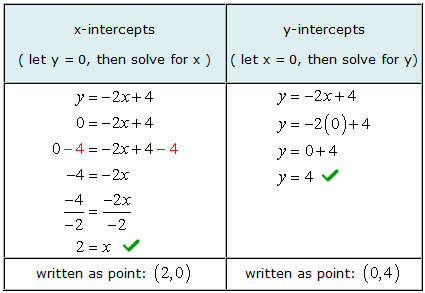
مثال 2: أوجد تقاطع x و y للخط المستقيم و = –2س + 4.

لإيجاد تقاطع x جبريًا, نحن نسمح و = 0 في المعادلة ثم حل لقيم س. بنفس الاسلوب, للبحث عن تقاطع y جبريًا, نحن نسمح س = 0 في المعادلة ثم حل من أجل و.

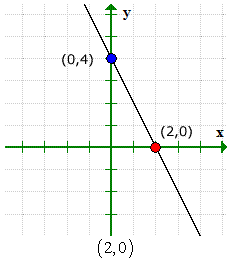
هذا الرسم البياني للتحقق من صحة إجاباتنا.

مثال 3: أوجد تقاطع x و y للمعادلة التربيعية و = س² - 2س - 3.

الرسم البياني لهذه المعادلة التربيعية هو القطع المكافئ. نتوقع أن يكون له شكل "U" حيث يفتح أو ينخفض.

لإيجاد تقاطع إكس لهذه المسألة, سوف تفعلها عامل ثلاثي الحدود بسيط. ثم تقوم بتعيين كل عامل ذي حدين يساوي صفرًا وتجد قيمة x.

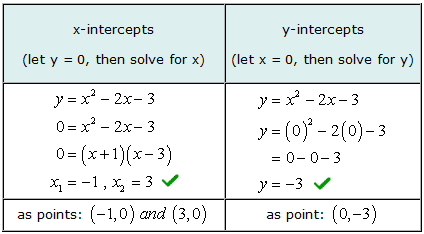
تتطابق القيم التي تم حلها لكل من تقاطع x و y مع الحل الرسومي.

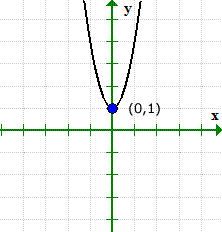
مثال 4: أوجد تقاطع x و y للمعادلة التربيعية و = 3س² + 1.

هذا مثال حيث يحتوي الرسم البياني للمعادلة على تقاطع ص ولكن بدون تقاطع س.

• لنجد تقاطع y أولاً لأنه سهل للغاية! قم بتوصيل x = 0 ثم حل من أجل y.

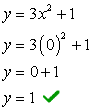
• الآن لتقاطع x. قم بتوصيل y = 0, وحل ل x.

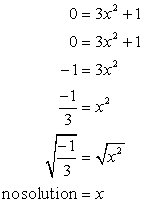
الجذر التربيعي لعدد سالب وهمي. هذا يشير إلى أن هذه المعادلة لا يمتلك تقاطع إكس!

يمكن للرسم البياني التحقق مما يحدث. لاحظ أن الرسم البياني يتقاطع مع المحور ص عند (0,1), لكنها لم تفعل مع المحور السيني.

مثال 5: أوجد مقطعي x و y للدائرة (س + 4)² + (و + 2)² = 8.

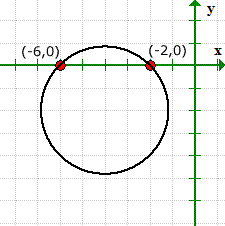
هذا مثال جيد لتوضيح أنه من الممكن أن يكون للرسم البياني للمعادلة تقاطعات س ولكن بدون تقاطعات ص.

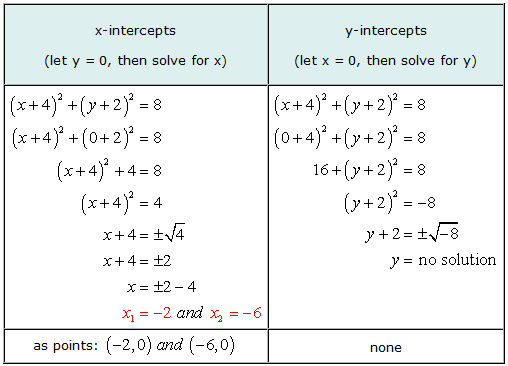
عند حل y, وصلنا إلى حالة محاولة الحصول على الجذر التربيعي لعدد سالب. الجواب خيالي, وهكذا, لا حل. هذا يعني أن المعادلة لا تحتوي على أي تقاطعات ص.

يتحقق الرسم البياني من أننا مناسبون لقيم تقاطعات x الخاصة بنا, وليس لها تقاطعات ص.

ائتمان:

HTTPS://www.studiosity.com/blog/

HTTPS://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/