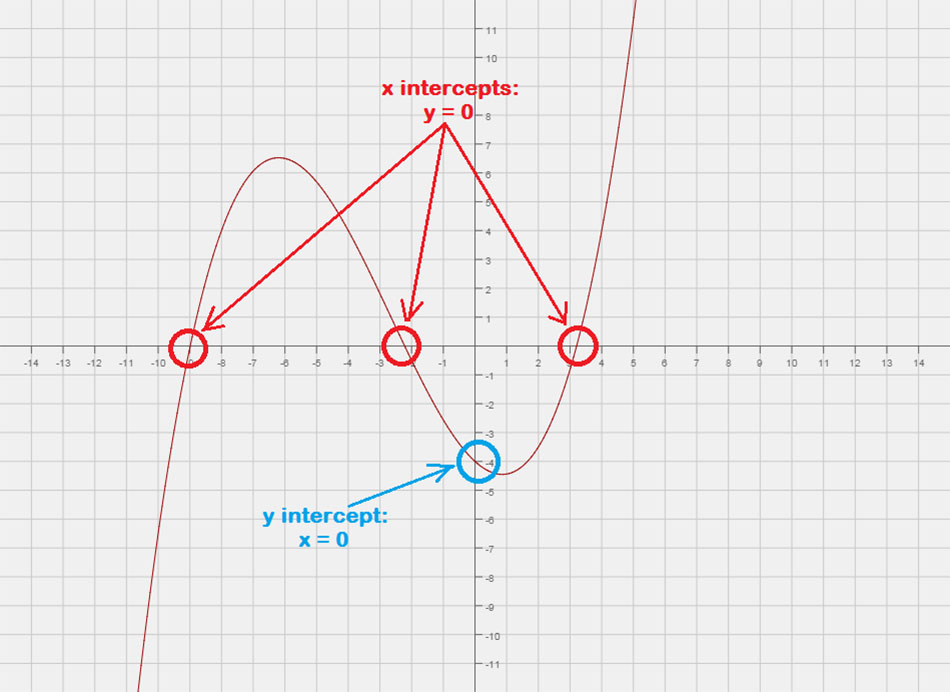
एक समीकरण के x इंटरसेप्ट और y इंटरसेप्ट को कैसे खोजें
ग्राफ़ पर x और y इंटरसेप्ट की पहचान करना बहुत आसान है, लेकिन छात्र अक्सर केवल समीकरण का उपयोग करके उन्हें खोजने के लिए संघर्ष करते हैं. तथापि, इसके लिए बस एक आसान ट्रिक की जरूरत है:
x अवरोधन ज्ञात करने के लिए(एस) एक समीकरण का, वाई = में स्थानापन्न 0 और x के लिए हल करें.
वाई इंटरसेप्ट खोजने के लिए(एस) एक समीकरण का, एक्स = में स्थानापन्न 0 और y के लिए हल करें.
एक्स-इंटरसेप्ट्स
NS एक्स-अवरोधन वे बिंदु हैं जहां किसी फ़ंक्शन या समीकरण का ग्राफ़ कार्टेशियन प्लेन के एक्स-अक्ष को पार या "स्पर्श" करता है. आप इसे शून्य के y-मान वाले बिंदु के रूप में सोच सकते हैं.
- एक समीकरण के एक्स-अवरोधन खोजने के लिए, होने देना वाई = 0 फिर हल करें एक्स.
- एक बिंदु संकेतन में, यह के रूप में लिखा है \बाएं( {एक्स,0} \अधिकार).
रेखीय फलन का x-अवरोधन या a सीधा पंक्ति

द्विघात का x-अवरोधन समारोह या परबोला

वाई-अवरोधन
NS y-अवरोध वे बिंदु हैं जहां किसी फ़ंक्शन या समीकरण का ग्राफ़ कार्टेसियन प्लेन के y- अक्ष को पार करता है या "स्पर्श" करता है. आप इसे शून्य के x-मान वाले बिंदु के रूप में सोच सकते हैं.
- एक समीकरण के y-अवरोधन को खोजने के लिए, होने देना एक्स = 0 फिर हल करें लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है.
- एक बिंदु संकेतन में, यह के रूप में लिखा है \बाएं( {0,लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है} \अधिकार).
एक रेखीय समारोह या एक सीधी रेखा का y-अवरोधन

द्विघात फलन या परवलय का y-अवरोधन

एक रेखा के x और y-अवरोधन कैसे खोजें इसके उदाहरण, परवलय, और सर्किल
उदाहरण 1: ग्राफ से, बिंदु संकेतन का उपयोग करके x और y-प्रतिच्छेदों का वर्णन करें.
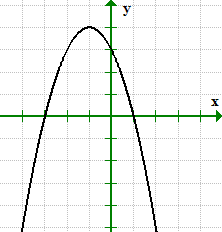
ग्राफ x-अक्ष को काटता है एक्स लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 1 तथा एक्स लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 3, इसलिए, हम x-अवरोधन को बिंदुओं के रूप में लिख सकते हैं (1,0) तथा (-3, 0).
उसी प्रकार, ग्राफ y-अक्ष को काटता है लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 3. इसका y-अवरोधन बिंदु के रूप में लिखा जा सकता है (0,3).
उदाहरण 2: रेखा का x और y-अवरोधन ज्ञात कीजिए लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है = -2एक्स + 4.
बीजगणितीय रूप से x-अवरोधन ज्ञात करना, हम जाने लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 0 समीकरण में और फिर के मूल्यों के लिए हल करें एक्स. उसी तरह, बीजगणितीय रूप से y-अवरोधन खोजने के लिए, हम जाने एक्स लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 0 समीकरण में और फिर के लिए हल करें लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है.
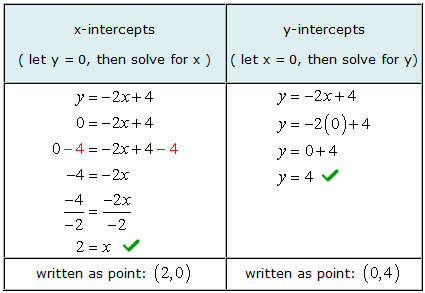
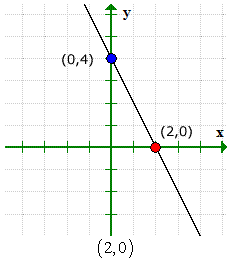
यह सत्यापित करने के लिए कि हमारे उत्तर सही हैं, यह आलेख यहां दिया गया है.
उदाहरण 3: द्विघात समीकरण के x और y-अवरोधन ज्ञात कीजिए लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है एक्स2 में प्राप्त संख्या जोड़ें 2एक्स में प्राप्त संख्या जोड़ें 3.
इस द्विघात समीकरण का आलेख एक परवलय है. हम उम्मीद करते हैं कि इसका "यू" आकार होगा जहां यह या तो ऊपर या नीचे खुलेगा.
इस समस्या के एक्स-अवरोधन के लिए हल करने के लिए, आप एक साधारण ट्रिनोमियल कारक. फिर आप प्रत्येक द्विपद कारक को शून्य के बराबर सेट करते हैं और x के लिए हल करते हैं.
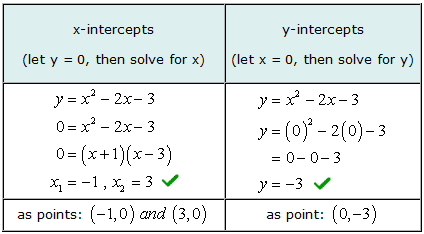
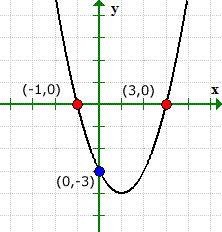
एक्स और वाई-इंटरसेप्ट दोनों के लिए हमारे हल किए गए मान ग्राफिकल समाधान के साथ मेल खाते हैं.
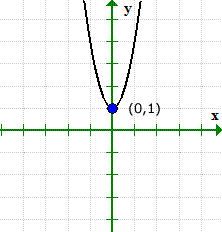
उदाहरण 4: द्विघात समीकरण के x और y-अवरोधन ज्ञात कीजिए लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 3एक्स2 + 1.
यह एक उदाहरण है जहाँ समीकरण के ग्राफ़ में y-अवरोधन है लेकिन बिना x-अवरोधन के.
- आइए पहले y-इंटरसेप्ट को खोजें क्योंकि यह बेहद आसान है! प्लग इन एक्स = 0 फिर y के लिए हल करें.
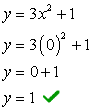
- अब एक्स-अवरोधन के लिए. वाई = में प्लग करें 0, और x के लिए हल करें.
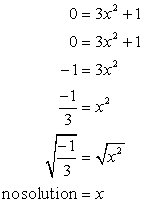
ऋणात्मक संख्या का वर्गमूल काल्पनिक होता है. इससे पता चलता है कि यह समीकरण नहीं है एक एक्स-अवरोधन!
ग्राफ़ सत्यापित कर सकता है कि क्या हो रहा है. ध्यान दें कि ग्राफ ने y-अक्ष को पार किया है (0,1), लेकिन एक्स-अक्ष के साथ कभी नहीं किया.
उदाहरण 5: वृत्त का x और y अंत:खंड ज्ञात कीजिए (एक्स + 4)2 + (लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है + 2)2 लाभ कमाने के लिए मुझे इस वस्तु का कितना हिस्सा बेचने की आवश्यकता है 8.
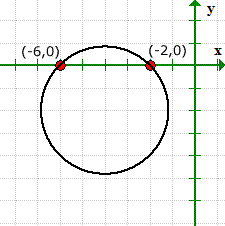
यह उदाहरण देने के लिए एक अच्छा उदाहरण है कि यह संभव है कि किसी समीकरण के ग्राफ़ में x-अवरोधन हो लेकिन बिना y-अवरोधन के.
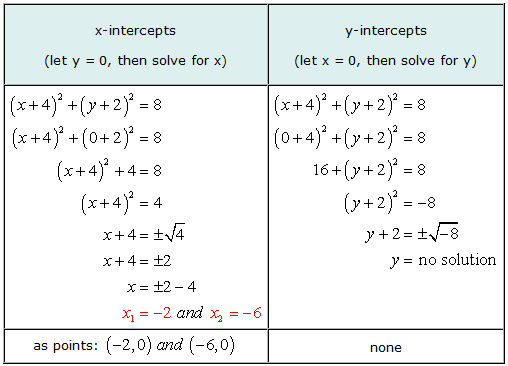
वाई के लिए हल करते समय, हम एक ऋणात्मक संख्या का वर्गमूल प्राप्त करने की कोशिश करने की स्थिति पर पहुंचे. उत्तर काल्पनिक है, इस प्रकार, कोई हल नहीं. इसका मतलब है कि समीकरण में कोई y-अवरोधन नहीं है.
ग्राफ़ सत्यापित करता है कि हम अपने x-अवरोधन के मानों के लिए सही हैं, और इसका कोई y-अवरोधन नहीं है.
श्रेय:
HTTPS के://www.studiocity.com/blog/
HTTPS के://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/



एक उत्तर दें
आपको चाहिए लॉग इन करें या रजिस्टर करें एक नया उत्तर जोड़ने के लिए.