Bardzo łatwo jest zidentyfikować punkty przecięcia osi x i y na wykresie, ale uczniowie często mają trudności z ich znalezieniem, używając tylko równania. Jednakże, wymaga to tylko prostej sztuczki:

Aby znaleźć punkt przecięcia x(s) równania, podstawnik w y = 0 i rozwiąż dla x.

Aby znaleźć punkt przecięcia y(s) równania, podstawnik w x = 0 i rozwiąż za y.

Przechwytywanie X

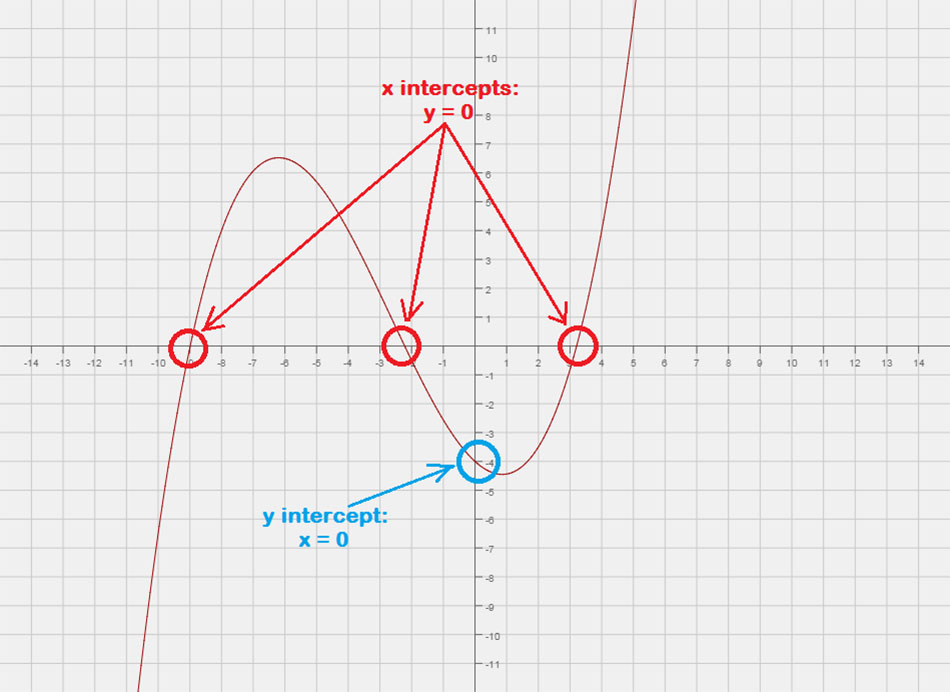
ten Przechwytywanie x są punktami, w których wykres funkcji lub równania przecina się lub „dotyka” osi x płaszczyzny kartezjańskiej. Możesz myśleć o tym jako o punkcie o wartości y równej zero.

• Aby znaleźć punkty przecięcia z osią x równania, pozwalać $Y=0$ następnie rozwiąż dla $x$.
• W notacji punktowej, jest napisane jako \lewo( {x,0} \Prawidłowy)(x,0).

przecięcie x funkcji liniowej lub a Prosty Linia

x-punkty przecięcia kwadratu Funkcjonować lub Parabola

Przechwytywanie Y

ten przechwytuje y to punkty, w których wykres funkcji lub równania przecina się lub „dotyka” osi y płaszczyzny kartezjańskiej. Możesz myśleć o tym jako o punkcie o wartości x równej zero.

• Aby znaleźć punkty przecięcia y równania, pozwalać $x=0$ następnie rozwiąż dla $Y$.
• W notacji punktowej, jest napisane jako \lewo( {0,Y} \Prawidłowy)(0,Y).

Punkt przecięcia y funkcji liniowej lub linii prostej

przecięcie y funkcji kwadratowej lub paraboli

Przykłady znajdowania punktów przecięcia osi x i y prostej, Parabola, i krąg

Przykład 1: Z wykresu, opisz punkty przecięcia osi x i y za pomocą notacji punktowej.

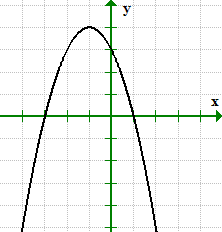
Wykres przecina oś x w x = 1 oraz x = 3, dlatego, możemy zapisać przecięcia z osią X jako punkty (1,0) oraz (–3, 0).

podobnie, wykres przecina oś y w Y = 3. Jego punkt przecięcia z osią y można zapisać jako punkt (0,3).

Przykład 2: Znajdź punkty przecięcia osi x i y prostej Y = –2x + 4.

Aby algebraicznie znaleźć punkty przecięcia z osią X, pozwalamy Y = 0 w równaniu, a następnie oblicz wartości x. W taki sam sposób, znaleźć algebraicznie dla przecięcia z osią y, pozwalamy x = 0 w równaniu, a następnie rozwiąż dla Y.

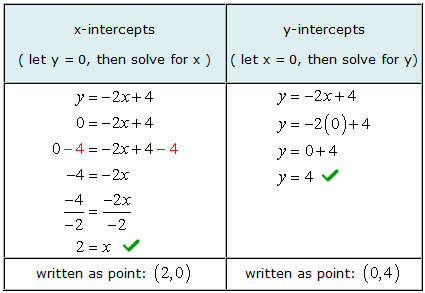
Oto wykres sprawdzający, czy nasze odpowiedzi są prawidłowe.

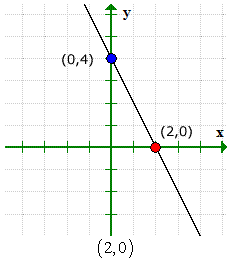
Przykład 3: Znajdź punkty przecięcia xiy równania kwadratowego Y = x² − 2x − 3.

Wykres tego równania kwadratowego to parabola. Spodziewamy się, że będzie miał kształt litery „U”, w którym będzie się otwierał lub opadał.

Aby znaleźć punkt przecięcia z osią X tego problemu, będziesz współczynnik prostego trójmianu. Następnie ustawiasz każdy czynnik dwumianowy równy zero i rozwiązujesz dla x.

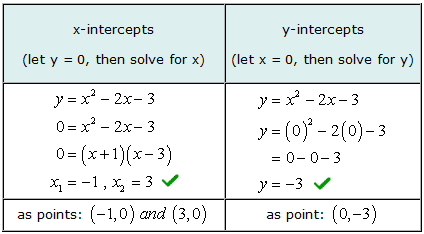
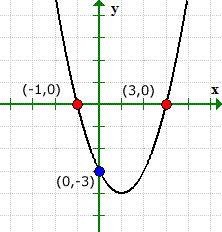
Nasze rozwiązane wartości dla punktów przecięcia osi x i y pasują do rozwiązania graficznego.

Przykład 4: Znajdź punkty przecięcia xiy równania kwadratowego Y = 3x² + 1.

To jest przykład, w którym wykres równania ma punkt przecięcia z osią y, ale bez punktu przecięcia z osią x.

• Najpierw znajdźmy punkt przecięcia Y, ponieważ jest to niezwykle łatwe! Podłącz x = 0 następnie znajdź y.

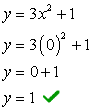
• Teraz do przecięcia osi X. Podłącz y = 0, i rozwiąż dla x.

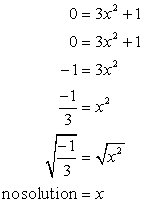
Pierwiastek kwadratowy z liczby ujemnej jest urojony. Sugeruje to, że to równanie nie ma punkt przecięcia osi X!

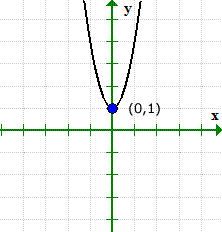
Wykres może zweryfikować, co się dzieje. Zauważ, że wykres przecina oś y w (0,1), ale nigdy nie robiłem z osią x.

Przykład 5: Znajdź punkty przecięcia osi x i y okręgu (x + 4)² + (Y + 2)² = 8.

Jest to dobry przykład ilustrujący, że wykres równania może mieć punkty przecięcia z osią X, ale bez punktów przecięcia z osią Y.

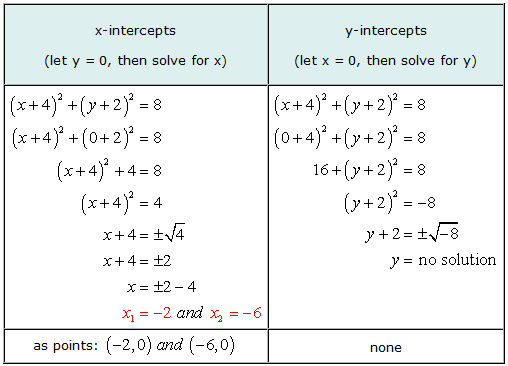
Rozwiązując dla y, doszliśmy do sytuacji, w której próbujemy obliczyć pierwiastek kwadratowy z liczby ujemnej. Odpowiedź jest urojona, zatem, brak rozwiązania. Oznacza to, że równanie nie ma żadnych punktów przecięcia z osią Y.

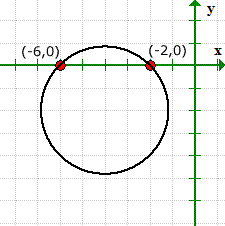
Wykres weryfikuje, czy mamy rację dla wartości naszych punktów przecięcia osi x, i nie ma przechwycenia y.

Kredyt:

https://www.studiosity.com/blog/

https://www.chiliath.com/lessons/intermediate-algebra/finding-x-y-intercepts/