Hva er mekanisk energi? Jeg trenger en omfattende definisjon
Hva er mekanisk energi
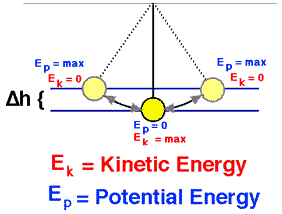 I fysikk, mekanisk energi (Emek) er energien knyttet til bevegelse og posisjon av et objekt vanligvis i et eller annet kraftfelt (f.eks. gravitasjonsfelt). Mekanisk energi (og også den termiske energien) kan deles inn i to kategorier, forbigående og lagret. Forbigående energi er energi i bevegelse, det er, energi som overføres fra et sted til et annet. Lagret energi er energien som finnes i et stoff eller en gjenstand. Forbigående mekanisk energi blir ofte referert til som arbeid. Lagret mekanisk energi finnes i en av to former: kinetisk eller potensiell:
I fysikk, mekanisk energi (Emek) er energien knyttet til bevegelse og posisjon av et objekt vanligvis i et eller annet kraftfelt (f.eks. gravitasjonsfelt). Mekanisk energi (og også den termiske energien) kan deles inn i to kategorier, forbigående og lagret. Forbigående energi er energi i bevegelse, det er, energi som overføres fra et sted til et annet. Lagret energi er energien som finnes i et stoff eller en gjenstand. Forbigående mekanisk energi blir ofte referert til som arbeid. Lagret mekanisk energi finnes i en av to former: kinetisk eller potensiell:
- Potensiell energi. Potensiell energi, U, er definert som energien som er lagret i et objekt utsatt for en konservativ kraft. Vanlige typer inkluderer gravitasjonspotensialenergien til et objekt som avhenger av dets masse og dets avstand fra massesenteret til et annet objekt.
- Kinetisk energi. Den kinetiske energien, K, er definert som energien som er lagret i et objekt på grunn av dets bevegelse. Det avhenger av hastigheten til et objekt og er evnen til et objekt i bevegelse til å utføre arbeid på andre objekter når det kolliderer med dem.
Bevaring av mekanisk energi
Først prinsippet om Bevaring av mekanisk energi ble oppgitt:
Den totale mekaniske energien (definert som summen av dens potensielle og kinetiske energier) av en partikkel som bare påvirkes av konservative krefter er konstant.
Grenoble Institute of Technology Foundation støtter et stipendprogram for internasjonale studenter som ønsker å forfølge et internasjonalt masterprogram ved Grenoble INP: Bevaring av mekanisk energi
Et isolert system er en der ingen ytre kraft forårsaker energiendringer. Hvis bare konservative krefter handle på en gjenstand og U er den potensiell energi funksjon for den totale konservative kraften, ikke-termisk stråling
Emek = U + K
Den potensielle energien, U, avhenger av posisjonen til et objekt utsatt for en konservativ kraft.
Det er definert som objektets evne til å utføre arbeid og økes når objektet beveges i motsatt retning av kraftens retning.
Den potensielle energien assosiert med et system som består av Jorden og en nærliggende partikkel er gravitasjonspotensialenergi.
Den kinetiske energien, K, avhenger av hastigheten til et objekt og er evnen til et objekt i bevegelse til å utføre arbeid på andre objekter når det kolliderer med dem.
K = mv2
Ovennevnte definisjon (Emek = U + K) antar at systemet er fri for friksjon og annen ikke-konservative krefter. Forskjellen mellom en konservativ og en ikke-konservativ kraft er at når en konservativ kraft flytter et objekt fra ett punkt til et annet, arbeidet utført av den konservative kraften er uavhengig av veien.
I enhver reell situasjon, friksjonskrefter og andre ikke-konservative krefter er til stede, men i mange tilfeller er deres virkninger på systemet så små at prinsippet om bevaring av mekanisk energi kan brukes som en rettferdig tilnærming. For eksempel er friksjonskraften en ikke-konservativ kraft, fordi det virker for å redusere den mekaniske energien i et system.
Merk at ikke-konservative krefter ikke alltid reduserer den mekaniske energien. En ikke-konservativ kraft endrer den mekaniske energien, det er krefter som øker den totale mekaniske energien, som kraften fra en motor eller motor, er også en ikke-konservativ kraft.
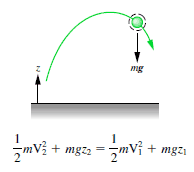
Blokk som glir ned en friksjonsfri skråning
De 1 kg blokk starter en høyde H (la si 1 m) over bakken, med potensiell energi mgH og kinetisk energi som er lik 0. Den glir til bakken (uten friksjon) og kommer uten potensiell energi og kinetisk energi K = mv2. Beregn hastigheten til blokken på bakken og dens kinetiske energi.
Emek = U + K = konst
=> ½ mv2 = mgH
=> v = √2gH = 4.43 m/s
=> K2 = ½ x 1 kg x (4.43 m/s)2 = 19.62 kg.m2.s-2 = 19.62 J
Pendel
 Anta a pendel (ball med masse m opphengt i en lengdestreng L at vi har trukket opp slik at ballen er en høyde H < L over det laveste punktet på buen for den strakte strengbevegelsen. Pendelen er utsatt for konservativ gravitasjonskraft hvor friksjonskrefter som luftmotstand og friksjon ved dreiepunktet er ubetydelige.
Anta a pendel (ball med masse m opphengt i en lengdestreng L at vi har trukket opp slik at ballen er en høyde H < L over det laveste punktet på buen for den strakte strengbevegelsen. Pendelen er utsatt for konservativ gravitasjonskraft hvor friksjonskrefter som luftmotstand og friksjon ved dreiepunktet er ubetydelige.
Vi slipper den fra hvile. Hvor fort går det i bunnen?
Pendelen når størst kinetisk energi og minst potensiell energi når i vertikal posisjon, fordi den vil ha størst hastighet og være nærmest jorden på dette tidspunktet. På den andre siden, det vil ha sitt minst kinetisk energi og størst potensiell energi de har redusert evne til å bøye ankelen og løfte foten ekstreme stillinger av svingen sin, fordi den har null hastighet og er lengst fra jorden på disse punktene.
Hvis amplituden er begrenset til små svingninger, perioden T av en enkel pendel, tiden det tar for en fullstendig syklus, er:
hvor L er lengden på pendelen og g er den lokale tyngdeakselerasjonen. For små husker er svingeperioden omtrent den samme for husker i forskjellige størrelser. Det er, perioden er uavhengig av amplitude.



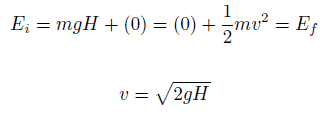
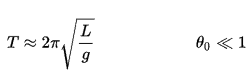
Legg igjen et svar
Du må Logg Inn eller registrere for å legge til et nytt svar.