Det er veldig enkelt å identifisere x- og y-avskjæringene på en graf, men elevene sliter ofte med å finne dem ved å bruke bare ligningen. derimot, det krever bare et enkelt triks:

For å finne x-skjæringspunktet(s) av en ligning, erstatte i y = 0 og løs for x.

For å finne y-skjæringen(s) av en ligning, erstatte i x = 0 og løse for y.

X-Intercepts

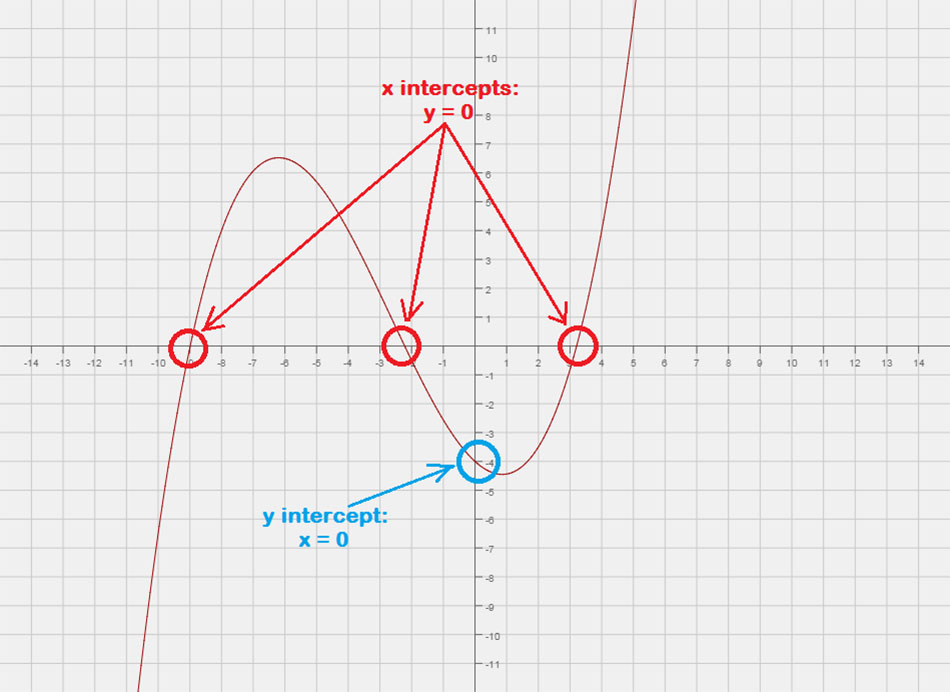
De x-avskjærer er punkter der grafen til en funksjon eller en ligning krysser eller "rører" x-aksen til det kartesiske planet. Du kan tenke på dette som et punkt med y-verdien null.

• For å finne x-skjæringspunktene til en ligning, la $Y=0$ deretter løse for $x$.
• I en punktnotasjon, det er skrevet som \venstre( {x,0} \Ikke sant)(x,0).

x-skjæringspunktet for en lineær funksjon eller en Rett Linje

x-avskjæringer av en kvadratisk Funksjon eller parabel

Y-avskjæringene

De y-skjæringer er punkter der grafen til en funksjon eller en ligning krysser eller "rører" y-aksen til det kartesiske planet. Du kan tenke på dette som et punkt med x-verdien null.

• For å finne y-avskjæringene til en ligning, la $x=0$ deretter løse for $Y$.
• I en punktnotasjon, det er skrevet som \venstre( {0,Y} \Ikke sant)(0,Y).

y-skjæringspunktet for en lineær funksjon eller en rett linje

y-skjæringspunktet for en kvadratisk funksjon eller parabel

Eksempler på hvordan finne x- og y-skjæringspunktene til en linje, Parabel, og sirkel

Forskjellen er at 1: Fra grafen, beskriv x- og y-avskjæringene ved hjelp av punktnotasjon.

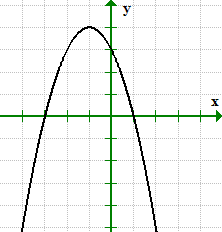
Grafen krysser x-aksen ved x = 1 og x = 3, derfor, vi kan skrive x-skjæringspunktene som punkter (1,0) og (–3, 0).

på samme måte, grafen krysser y-aksen ved Y = 3. Y-skjæringspunktet kan skrives som punktet (0,3).

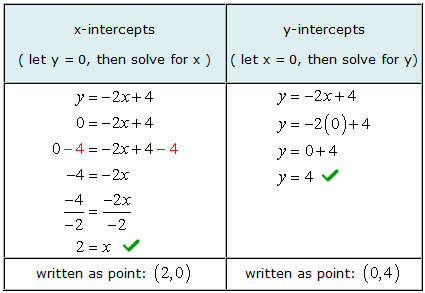
Forskjellen er at 2: Finn x- og y-skjæringspunktene til linjen Y = –2x + 4.

Å finne x-skjæringspunktene algebraisk, vi lar Y = 0 i ligningen og løs deretter for verdier av x. På samme måte, å finne for y-avskjæringer algebraisk, vi lar x = 0 i ligningen og løs deretter for Y.

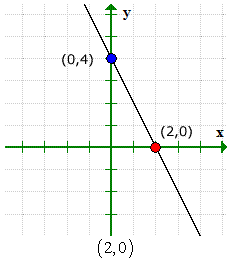
Her er grafen for å bekrefte at svarene våre er riktige.

Forskjellen er at 3: Finn x- og y-avskjæringene til andregradsligningen Y = x² − 2x − 3.

Grafen til denne kvadratiske ligningen er en parabel. Vi forventer at den har en "U"-form der den enten vil åpne seg opp eller ned.

For å løse x-skjæringspunktet til dette problemet, du vil faktor et enkelt trinomium. Deretter setter du hver binomialfaktor lik null og løser for x.

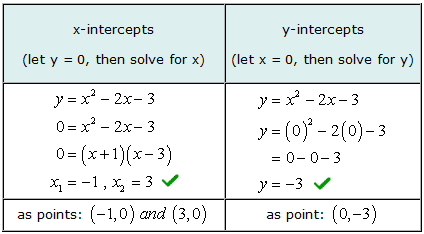
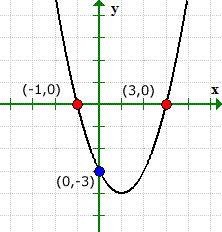
Våre løste verdier for både x- og y-avskjæringer samsvarer med den grafiske løsningen.

Forskjellen er at 4: Finn x- og y-avskjæringene til andregradsligningen Y = 3x² + 1.

Dette er et eksempel hvor grafen til ligningen har et y-skjæringspunkt, men uten et x-skjæringspunkt.

• La oss finne y-skjæringspunktet først fordi det er ekstremt enkelt! Plugg inn x = 0 løs deretter for y.

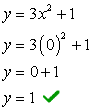
• Nå for x-skjæringspunktet. Plugg inn y = 0, og løs for x.

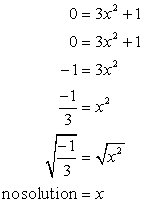
Kvadratroten av et negativt tall er imaginær. Dette antyder at denne ligningen har ikke et x-skjæringspunkt!

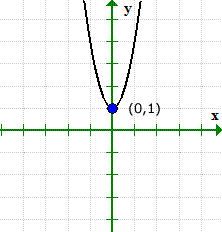
Grafen kan bekrefte hva som skjer. Legg merke til at grafen krysset y-aksen ved (0,1), men gjorde det aldri med x-aksen.

Forskjellen er at 5: Finn x- og y-skjæringspunktene til sirkelen (x + 4)² + (Y + 2)² = 8.

Dette er et godt eksempel for å illustrere at det er mulig for grafen til en ligning å ha x-avskjæringer, men uten y-avskjæringer.

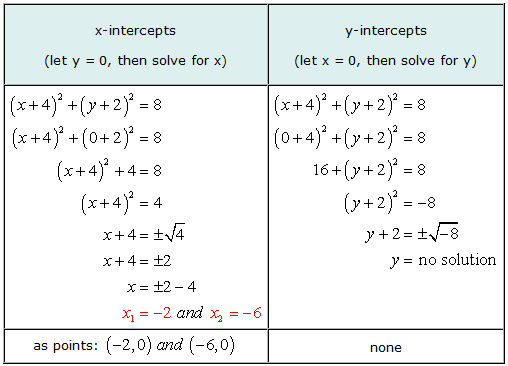
Ved løsning for y, vi kom frem til situasjonen med å prøve å få kvadratroten av et negativt tall. Svaret er imaginært, og dermed, ingen løsning. Det betyr at ligningen ikke har noen y-avskjæringer.

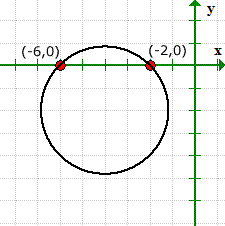
Grafen bekrefter at vi har rett for verdiene til x-avskjæringene våre, og den har ingen y-avskjæringer.

Kreditt:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/