Hva er det virkelige livsscenariet som involverer kvadratiske ligninger?
Det er mange virkelige situasjoner som involverer quadratics og parabolas. Kaste en ball, skyte en kanon, dykking av en plattform, og å slå en golfball er alle eksempler på situasjoner som kan simuleres ved hjelp av kvadratiske funksjoner.
Den kvadratiske ligningen brukes praktisk talt i astronomi, matematikk, ingeniørfag, medisin, finansiere, skogbruk, vitenskap eller forskning, etc. På ethvert felt, hvis det er en akademisk eller forskningsaktivitet, det vil sannsynligvis være et ligningssystem som kan kreve en kvadratisk ligning å løse.
For det vanlige livet, uten bruk av akademisk materiale, matematikk eller ligninger er ikke nødvendig; og, derfor, en kvadratisk ligning er ikke nødvendig.
Du vil bli overrasket over antall applikasjoner som bruker kvadratiske ligninger.
Kast en ball i luften. Buen den følger er en parabel. Og en parabel kan representeres av en andregradsligning.
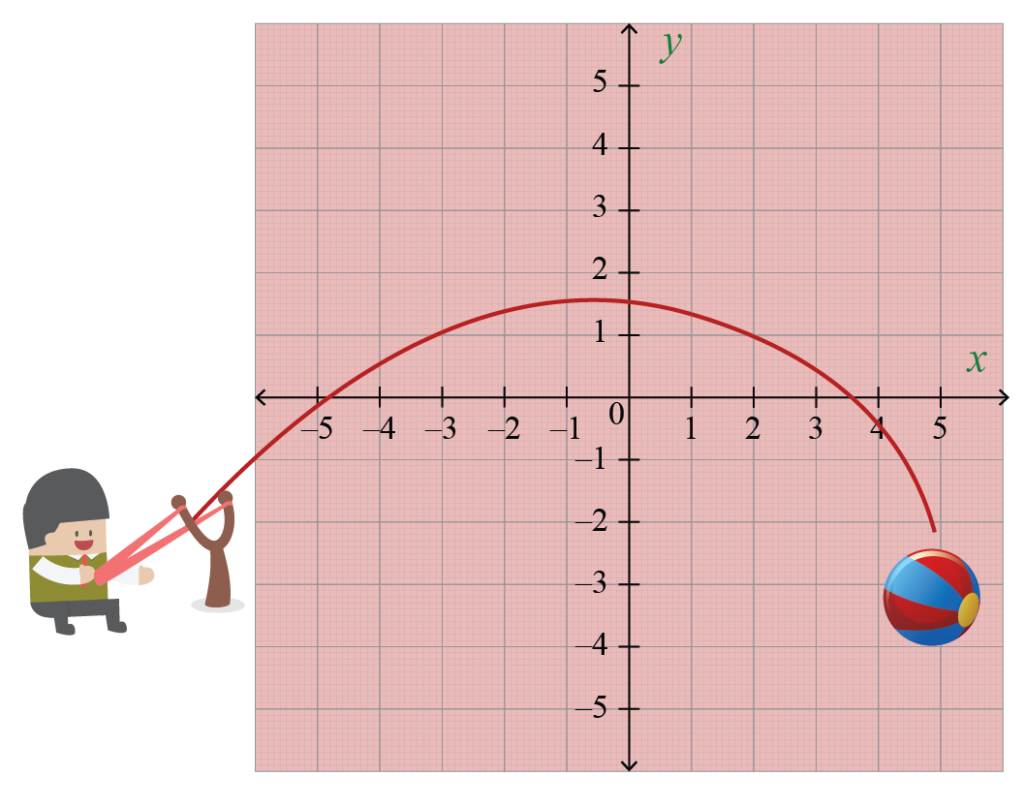
Hva er fokuset til en parabel? En måte å definere en parabel på er at den er settet med punkter i planet like langt fra en gitt linje, kalt dirigeren, og et gitt punkt, kalt fokus.
Hvordan brukes kvadratiske ligninger i hverdagen vår?
Kvadratiske ligninger brukes ofte i hverdagen. Tyngdekraften er proporsjonal med det omvendte kvadratet av avstanden fra Jorden, altså prosjektiler, fra en tennisball til en rakett, fly langs en parabolsk bane.
Anta at du vil røre kaffe, centripetalkraften til kaffe er kvadratisk i naturen, så når du fjerner skjeen, du skjønner at den danner en paraboloid form (forestill deg en tredimensjonal parabel).
Kvadratiske ligninger brukes ofte i optimaliseringsproblemer både innen ingeniørfag og finans, når du ønsker å minimere kostnadene for en bestemt vare eller maksimere fortjenesten, og noen ganger kan dette modelleres ved andregradsligninger (om enn ikke alltid).
Måten å bestemme motstanden til motstandene parallelt krever en fungerende forståelse av å løse andregradsligninger, hvis du vet noen konklusjoner, så det er viktig å ha riktig kombinasjon av motstander for ikke å ødelegge viktige kretselementer.
Parabolske speil og mikrofoner bruker samme funksjon som paraboler og derfor paraboloider, som er at de kan konsentrere refleksjoner på ett punkt, som gir et veldig godt bilde for et teleskop eller et klart signal fra en mikrofon.
Nå noen fortsatt hverdagslige applikasjoner, men i større skala, er i andre ordens ODE-er, som krever en hjelpeligning for å løse, som er en andregradsligning, og hvis resultat bestemmer funksjonen for hele systemet.
Eksempler på bruk av denne ligningen er svinger som bruker enkel harmonisk bevegelse, som fjærene i bilen din eller fjærene i de fleste mekaniske enheter på bakken.
Opprinnelsen til kvadratisk ligning
Babylonerne var de første som oppfant kvadratiske ligninger så langt tilbake som 2000 f.Kr.. De trengte dem for landbruks- og vanningsberegninger.
Grekerne brukte dem senere – Arkimedes tydde til dem for å finne verdien av radiusen til en sirkel.
I dag bruker vi dem hver dag for å beregne areal (størrelsen på en boks, en stue, en tomt), å bestemme fortjenesten til en vare (hvor mye av denne varen må jeg selge for å tjene penger?) eller for å estimere hastigheten til et objekt (hvis jeg kaster noe på deg – noe solid, – hvor lang tid vil det ta før det jeg kaster havner i hendene dine?)
Årsakene til at man ønsker å finne en løsning på slike problemer er ikke fullt ut kjent, men vi kan gjette.
For eksempel, de kan ha hatt en viss mengde materiale å omslutte et rektangulært felt av et gitt område med. Kanskje de trengte å vite hva den ideelle mengden materiale å bruke for den omkretsen var, eller om de fikk nok.
Uansett deres behov, de hadde en løsning på problemet. De skrev det ned trinn for trinn som følger:
x + Y =s; ………………………………………… (1)
xy=en; ……………………………………………. (2)
(1) Finn halvparten av s.
(2) Kvadrerer antallet oppnådd i 1.
(3) Trekk tallet du finner i 2 av en.
(4) Finn kvadratroten til tallet du finner i 3.
(5) Legg til nummeret som er oppnådd i 1 til tallet oppnådd i 4. Dette er lengden på en av sidene.
Utfører trinn 4 var den vanskeligste delen, selv om det er kjent at babylonerne har brukt firkantede bord, antagelig inneholdende en liste med firkantede tall, for å tilnærme kvadratroten til et tall.
Noen historikere tilskriver også babylonerne den aller første anvendelsen av Newtons metode, som ble brukt spesifikt for å finne kvadratrøtter.
Det interessante med alt dette er hvordan den kvadratiske formelen (∗) oppsto av et slikt problem. Tross alt, vi løser ikke en kvadratisk ligning her, men et par samtidige ligninger (1) og (2).
Dette er ikke vanskelig å se, bruker dagens notasjoner. Fra (1) vi får y = s-x, som når erstattet med (2) gir:
x(s−x)=en.
sx−x2=en.
x2−sx+en=0.
Og dermed, (1) og (2) tilsvarer å løse den kvadratiske ligningen x2-sx + a = 0. nærmere bestemt, dette forteller oss at i denne kvadratiske ligningen, koeffisienten til x er den negative av summen av de to løsningene (ligning (1) ), og koeffisienten til en er produktet av de to løsningene (ligning (2) ).



Legg igjen et svar
Du må Logg Inn eller registrere for å legge til et nytt svar.