What Are The Real Life Scenario Involving Quadratic Equations?
There are a lot of real situations involving quadratics and parabolas. Throwing a ball, shooting a cannon, diving off a platform, and hitting a golf ball are all examples of situations that can be simulated using quadratic functions.
The quadratic equation is practically used in astronomy, mathematics, engineering, medicine, finance, forestry, science or research, etc. In any field, if there is an academic or research activity, there is likely to be a system of equations that may require a quadratic equation to solve.
For ordinary life, without the use of any academic materials, mathematics or equations are not needed; and, therefore, a quadratic equation is not required.
You’ll be surprised by the number of applications that use quadratic equations.
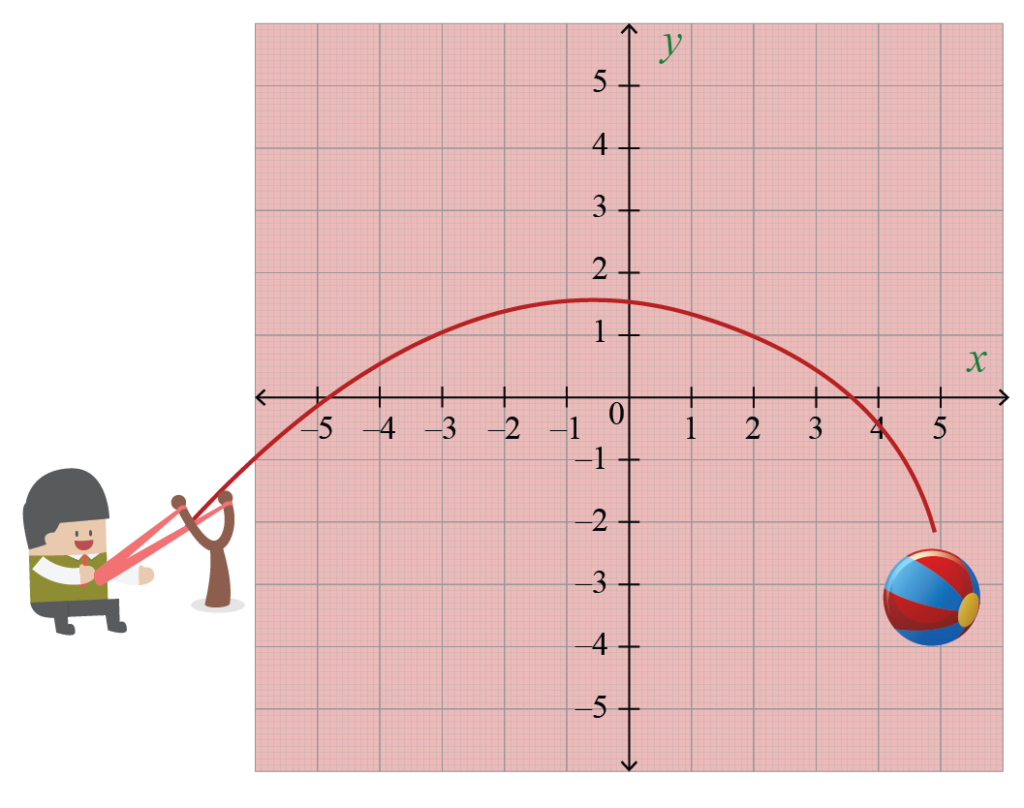
Throw a ball in the air. The arc it follows is a parabola. And a parabola can be represented by a quadratic equation.
What is the focus of a parabola? One way to define a parabola is that it is the set of points in the plane equidistant from a given line, called the directrix, and a given point, called the focus.
How are quadratic equations applied in our everyday life?
Quadratic equations are often used in everyday life. The force of gravity is proportional to the inverse square of the distance from Earth, so projectiles, from a tennis ball to a rocket, fly along a parabolic trajectory.
Suppose you want to stir coffee, the centripetal force of coffee is quadratic in nature, so when you remove the spoon, you realize that it forms a paraboloid shape (imagine a three-dimensional parabola).
Quadratic equations are often used in optimization problems in both engineering and finance, when you want to minimize the cost of a particular good or maximize profit, and sometimes this can be modeled by quadratic equations (though not always).
The way to determine the resistance of the resistors in parallel requires a working understanding of solving quadratic equations, if you know some conclusions, so it is important to have the right combination of resistors so as not to destroy important circuit elements.
Parabolic mirrors and microphones use the same feature of parabolas and therefore paraboloids, which is that they can concentrate reflections at one point, which gives a very good image for a telescope or a clear signal from a microphone.
Now some still everyday applications, but on a larger scale, are in 2nd order ODEs, which require an auxiliary equation to solve, which is a quadratic equation, and whose result determines the function for the whole system.
Examples of uses of this equation are swings that use simple harmonic motion, like the springs in your car or the springs in most mechanical devices on the ground.
Origin Of Quadratic Equation
The Babylonians were the first to invent quadratic equations as far back as 2000BC. They needed them for agricultural and irrigation calculations.
The Greeks used them later – Archimedes resorted to them to find the value of the radius of a circle.
Today we use them every day to calculate area (the size of a box, a living room, a plot of land), to determine the profit of a commodity (how much of this commodity do I need to sell to make a profit?) or to estimate the speed of an object (if I throw something at you – something solid, – how long will it take for what I throw to end up in your hands?)
The reasons for wanting to find a solution to such problems are not fully known, but we can make guesses.
For example, they may have had a certain amount of material with which to enclose a rectangular field of a given area. Perhaps they needed to know what the ideal amount of material to use for that perimeter was, or if they had enough.
Whatever their needs, they did have a solution to the problem. They wrote it down step by step as follows:
x + y =s; ………………………………………… (1)
xy=a; ……………………………………………. (2)
(1) Find half of s.
(2) Square the number obtained in 1.
(3) Subtract the number found in 2 by a.
(4) Find the square root of the number found in 3.
(5) Add the number obtained in 1 to the number obtained in 4.This is the length of one of the sides.
Performing step 4 was the hardest part, although the Babylonians are known to have used square tables, presumably containing a list of square numbers, to approximate the square root of a number.
Some historians also attribute to the Babylonians the very first application of Newton’s method, which was used specifically to find square roots.
The interesting thing about all this is how the quadratic formula (∗) arose from such a problem. After all, we are not solving a quadratic equation here, but a pair of simultaneous equations (1) and (2).
This is not hard to see, using today’s notations. From (1) we get y=s-x, which when substituted into (2) gives:
x(s−x)=a.
sx−x2=a.
x2−sx+a=0.
Thus, (1) and (2) are equivalent to solving the quadratic equation x2-sx+a=0. Specifically, this tells us that in this quadratic equation, the coefficient of x is the negative of the sum of the two solutions (equation (1) ), and the coefficient of one is the product of the two solutions (equation (2) ).



Leave an answer
You must login or register to add a new answer.