ง่ายมากที่จะระบุจุดตัด x และ y บนกราฟ, แต่นักเรียนมักพยายามหาพวกเขาโดยใช้สมการเท่านั้น. อย่างไรก็ตาม, แค่มีทริคง่ายๆ:

เพื่อหาจุดตัด x(NS) ของสมการ, แทนด้วย y = 0 และแก้หา x.

เพื่อหาจุดตัดแกน y(NS) ของสมการ, แทน x = 0 และแก้หา y.

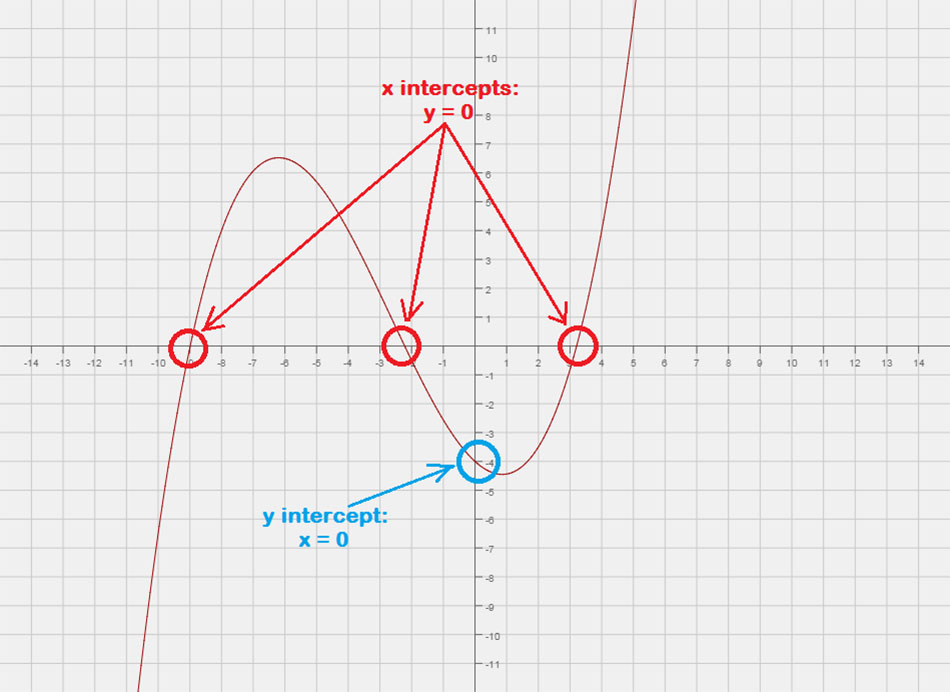
X-Intercepts

NS x-ตัดกัน คือจุดที่กราฟของฟังก์ชันหรือสมการตัดกันหรือ "สัมผัส" แกน x ของระนาบคาร์ทีเซียน. คุณอาจคิดว่าเป็นจุดที่มีค่า y เป็นศูนย์.

• การหาจุดตัดแกน x ของสมการ, อนุญาต $Y=0$ แล้วแก้ปัญหาสำหรับ $NS$.
• ในสัญกรณ์จุด, มันเขียนว่า \ซ้าย( {NS,0} \ขวา)(NS,0).

ค่าตัดแกน x ของฟังก์ชันเชิงเส้นหรือ ตรง เส้น

จุดตัดแกน x ของกำลังสอง การทำงาน หรือพาราโบลา

Y-Intercepts

NS y-ตัดกัน คือจุดที่กราฟของฟังก์ชันหรือสมการตัดกันหรือ "สัมผัส" แกน y ของระนาบคาร์ทีเซียน. คุณอาจคิดว่าเป็นจุดที่มีค่า x เป็นศูนย์.

• ในการหาจุดตัดแกน y ของสมการ, อนุญาต $NS=0$ แล้วแก้ปัญหาสำหรับ $Y$.
• ในสัญกรณ์จุด, มันเขียนว่า \ซ้าย( {0,Y} \ขวา)(0,Y).

จุดตัดแกน y ของฟังก์ชันเชิงเส้นหรือเส้นตรง

จุดตัดแกน y ของฟังก์ชันกำลังสองหรือพาราโบลา

ตัวอย่างวิธีการหาจุดตัดแกน x และ y ของเส้นตรง, พาราโบลา, และวงกลม

ตัวอย่าง 1: จากกราฟ, อธิบายจุดตัดแกน x และ y โดยใช้เครื่องหมายจุด.

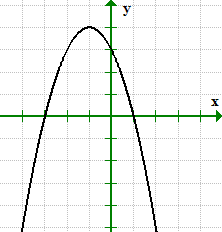
กราฟตัดแกน x ที่ NS = 1 และ NS = 3, ดังนั้น, เราเขียนจุดตัดแกน x เป็นจุดได้ (1,0) และ (–3, 0).

ซึ่งเชื่อว่าจะเป็นประโยชน์ต่อการส่งมอบยาที่ต้องฉีดต่อไปในระยะยาว, กราฟตัดแกน y ที่ Y = 3. ค่าตัดแกน y สามารถเขียนเป็นจุดได้ (0,3).

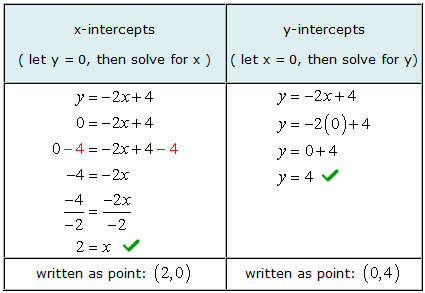
ตัวอย่าง 2: หาจุดตัดแกน x และ y ของเส้นตรง Y = –2NS + 4.

ในการหาค่าตัดแกน x ในทางพีชคณิต, เราปล่อยให้ Y = 0 ในสมการแล้วแก้หาค่าของ NS. ในลักษณะเดียวกัน, เพื่อหาค่าตัดแกน y ในทางพีชคณิต, เราปล่อยให้ NS = 0 ในสมการแล้วแก้หา Y.

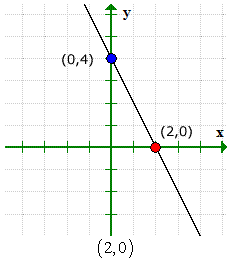
นี่คือกราฟเพื่อตรวจสอบว่าคำตอบของเราถูกต้อง.

ตัวอย่าง 3: หาจุดตัดแกน x และ y ของสมการกำลังสอง Y = NS² − 2NS − 3.

กราฟของสมการกำลังสองนี้เป็นพาราโบลา. เราคาดว่าจะมีรูปร่าง "U" ซึ่งจะเปิดขึ้นหรือลง.

ในการหาค่าตัดแกน x ของปัญหานี้, คุณจะ แยกตัวประกอบไตรนามอย่างง่าย. จากนั้นคุณตั้งค่าตัวประกอบทวินามแต่ละตัวให้เท่ากับศูนย์และแก้หาค่า x.

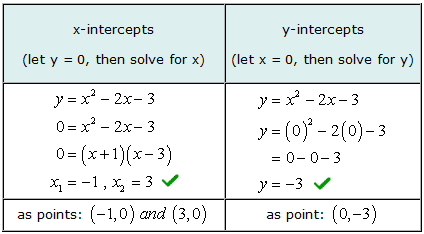
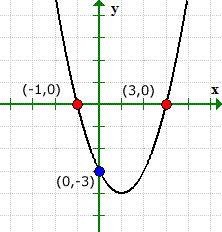
ค่าที่แก้ไขของเราสำหรับทั้ง x และ y-intercepts ตรงกับวิธีแก้ปัญหาแบบกราฟิก.

ตัวอย่าง 4: หาจุดตัดแกน x และ y ของสมการกำลังสอง Y = 3NS² + 1.

นี่คือตัวอย่างที่กราฟของสมการมีจุดตัดแกน y แต่ไม่มีจุดตัดแกน x.

• หาจุดตัดแกน y ก่อนเพราะมันง่ายมาก! เสียบ x = 0 แล้วแก้หา y.

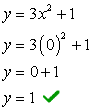
• ตอนนี้สำหรับ x-intercept. เสียบ y = 0, และแก้หา x.

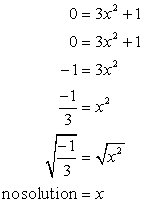
รากที่สองของจำนวนลบเป็นจำนวนจินตภาพ. แสดงว่าสมการนี้ ไม่ได้มี จุดตัดแกน x!

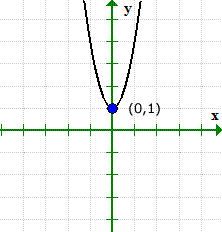
กราฟสามารถตรวจสอบสิ่งที่เกิดขึ้นได้. สังเกตว่ากราฟตัดแกน y ที่ (0,1), แต่ไม่เคยทำกับแกน x.

ตัวอย่าง 5: ค้นหาจุดตัดแกน x และ y ของวงกลม (NS + 4)² + (Y + 2)² = 8.

นี่เป็นตัวอย่างที่ดีที่แสดงให้เห็นว่าเป็นไปได้ที่กราฟของสมการจะมีจุดตัดแกน x แต่ไม่มีจุดตัดแกน y.

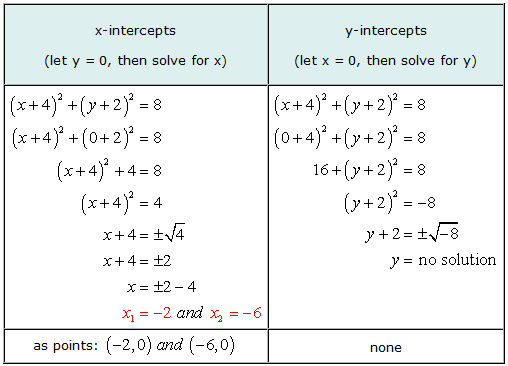
เมื่อแก้ปัญหาสำหรับ y, เรามาถึงสถานการณ์ของการพยายามหารากที่สองของจำนวนลบ. คำตอบคือจินตนาการ, ดังนั้น, ไม่มีวิธีแก้ปัญหา. นั่นหมายความว่าสมการไม่มีจุดตัดแกน y.

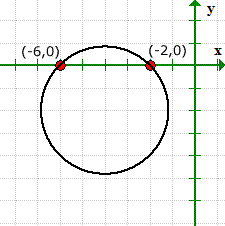
กราฟยืนยันว่าเราถูกต้องสำหรับค่าของจุดตัดแกน x, และไม่มีจุดตัดแกน y.

เครดิต:

https://www.studiosity.com/blog/

https://www.chilimath.com/lessons/intermediate-algebra/finding-x-y-intercepts/