อะไรคือสถานการณ์ชีวิตจริงที่เกี่ยวข้องกับสมการกำลังสอง?
มีสถานการณ์จริงมากมายที่เกี่ยวข้องกับสมการกำลังสองและพาราโบลา. ขว้างลูกบอล, ยิงปืนใหญ่, กระโดดลงจากแท่น, และการตีลูกกอล์ฟล้วนเป็นตัวอย่างสถานการณ์ที่สามารถจำลองได้โดยใช้ฟังก์ชันกำลังสอง.
สมการกำลังสองนี้ใช้ได้จริงในทางดาราศาสตร์, คณิตศาสตร์, วิศวกรรม, ยา, การเงิน, ป่าไม้, วิทยาศาสตร์หรือการวิจัย, ฯลฯ. ในทุกสาขา, หากมีกิจกรรมทางวิชาการหรือการวิจัย, มีแนวโน้มว่าจะมีระบบสมการที่อาจต้องใช้สมการกำลังสองในการแก้สมการ.
เพื่อชีวิตธรรมดาๆ, โดยไม่ต้องใช้สื่อวิชาการใดๆ, คณิตศาสตร์หรือสมการไม่จำเป็น; และ, ดังนั้น, ไม่จำเป็นต้องมีสมการกำลังสอง.
คุณจะประหลาดใจกับจำนวนแอพพลิเคชั่นที่ใช้สมการกำลังสอง.
โยนลูกบอลขึ้นไปในอากาศ. ส่วนโค้งที่ตามมาคือพาราโบลา. และพาราโบลาสามารถแทนด้วยสมการกำลังสองได้.
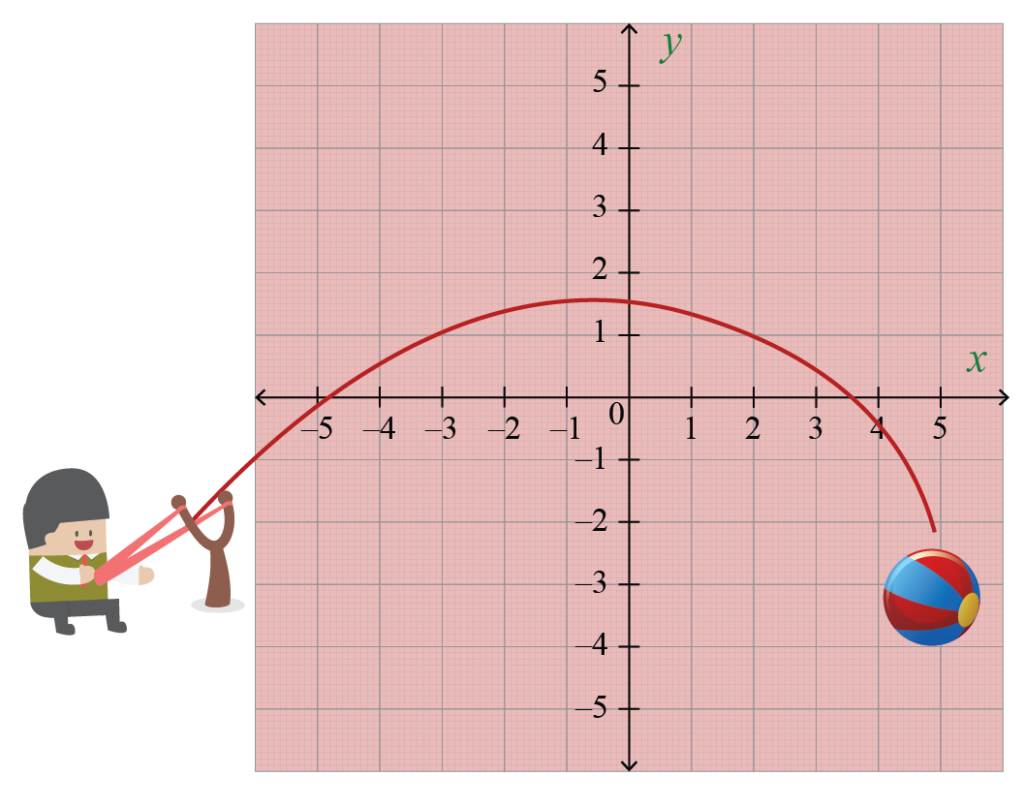
จุดเน้นของพาราโบลาคืออะไร? วิธีหนึ่งในการนิยามพาราโบลาคือ มันคือเซตของจุดในระนาบที่เท่ากันกับเส้นที่กำหนด, เรียกว่าไดเรกทริกซ์, และจุดที่กำหนด, เรียกว่าโฟกัส.
สมการกำลังสองถูกนำมาใช้ในชีวิตประจำวันของเราอย่างไร?
สมการกำลังสองมักใช้ในชีวิตประจำวัน. แรงโน้มถ่วงเป็นสัดส่วนกับกำลังสองผกผันของระยะห่างจากโลก, ดังนั้นขีปนาวุธ, จากลูกเทนนิสสู่จรวด, บินไปตามวิถีพาราโบลา.
สมมติว่าคุณต้องการกวนกาแฟ, แรงสู่ศูนย์กลางของกาแฟเป็นกำลังสองในธรรมชาติ, ดังนั้นเมื่อคุณเอาช้อนออก, คุณตระหนักว่ามันสร้างรูปทรงพาราโบลา (ลองนึกภาพพาราโบลาสามมิติ).
สมการกำลังสองมักใช้ในปัญหาการปรับให้เหมาะสมทั้งในด้านวิศวกรรมและการเงิน, เมื่อคุณต้องการลดต้นทุนของสินค้าบางรายการหรือเพิ่มผลกำไรสูงสุด, และบางครั้งสามารถจำลองได้ด้วยสมการกำลังสอง (แม้ว่าจะไม่เสมอไป).
วิธีการกำหนดความต้านทานของตัวต้านทานแบบขนานนั้นต้องใช้ความเข้าใจในการแก้สมการกำลังสอง, ถ้าคุณรู้ข้อสรุปบางอย่าง, ดังนั้นจึงเป็นสิ่งสำคัญที่จะต้องมีตัวต้านทานผสมกันที่เหมาะสมเพื่อไม่ให้องค์ประกอบวงจรที่สำคัญเสียหาย.
กระจกเงาและไมโครโฟนแบบพาราโบลาใช้คุณลักษณะเดียวกันกับพาราโบลาและดังนั้นจึงเป็นพาราโบลา, คือสามารถรวมสมาธิไว้ที่จุดหนึ่งได้, ซึ่งให้ภาพที่ดีมากสำหรับกล้องโทรทรรศน์หรือสัญญาณที่ชัดเจนจากไมโครโฟน.
ตอนนี้บางแอปพลิเคชันยังคงทุกวัน, แต่ในระดับที่ใหญ่กว่า, อยู่ในลำดับที่ 2 ODEs, ซึ่งต้องใช้สมการช่วยแก้, ซึ่งเป็นสมการกำลังสอง, และผลลัพธ์เป็นตัวกำหนดหน้าที่ของทั้งระบบ.
ตัวอย่างการใช้สมการนี้คือ วงสวิงที่ใช้การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย, เช่นสปริงในรถของคุณหรือสปริงในอุปกรณ์ทางกลส่วนใหญ่บนพื้นดิน.
ที่มาของสมการกำลังสอง
ชาวบาบิโลนเป็นคนแรกที่คิดค้นสมการกำลังสองจนถึง 2000 ปีก่อนคริสตกาล. พวกเขาต้องการสำหรับการคำนวณทางการเกษตรและการชลประทาน.
ชาวกรีกใช้ในภายหลัง – อาร์คิมิดีสใช้พวกเขาเพื่อหาค่ารัศมีของวงกลม.
วันนี้เราใช้พวกมันทุกวันเพื่อคำนวณพื้นที่ (ขนาดกล่อง, ห้องนั่งเล่น, ที่ดิน), เพื่อกำหนดกำไรของสินค้าโภคภัณฑ์ (ฉันต้องขายสินค้านี้เท่าไหร่ถึงจะทำกำไรได้?) หรือประมาณความเร็วของวัตถุ (ถ้าฉันขว้างอะไรใส่คุณ – บางสิ่งที่มั่นคง, – อีกนานไหมกว่าของที่ฉันขว้างไปจะถึงมือเธอ?)
เหตุผลที่ต้องการหาทางแก้ไขปัญหาดังกล่าวยังไม่เป็นที่ทราบแน่ชัด, แต่เราเดาได้.
ตัวอย่างเช่น, พวกเขาอาจมีวัสดุจำนวนหนึ่งที่จะล้อมรอบสนามสี่เหลี่ยมของพื้นที่ที่กำหนด. บางทีพวกเขาอาจจำเป็นต้องรู้ว่าปริมาณวัสดุในอุดมคติที่จะใช้สำหรับปริมณฑลนั้นคืออะไร, หรือถ้าพอแล้ว.
แล้วแต่ความต้องการ, พวกเขามีวิธีแก้ไขปัญหา. พวกเขาเขียนทีละขั้นตอนดังนี้:
NS + Y =NS; ………………………………………… (1)
xy=เอ; ……………………………………………. (2)
(1) ค้นหาครึ่งหนึ่งของ NS.
(2) ยกกำลังสองจำนวนที่ได้รับใน 1.
(3) ลบตัวเลขที่พบใน 2 โดย เอ.
(4) หารากที่สองของตัวเลขที่พบใน 3.
(5) เพิ่มหมายเลขที่ได้รับใน 1 กับจำนวนที่ได้จาก 4 นี่คือความยาวของด้านใดด้านหนึ่ง.
ดำเนินการขั้นตอน 4 เป็นส่วนที่ยากที่สุด, แม้ว่าชาวบาบิโลนจะรู้จักใช้โต๊ะสี่เหลี่ยม, น่าจะมีรายการเลขกำลังสอง, เพื่อประมาณรากที่สองของตัวเลข.
นักประวัติศาสตร์บางคนยังถือว่าชาวบาบิโลนใช้วิธีการของนิวตันเป็นครั้งแรก, ซึ่งใช้เฉพาะในการหารากที่สอง.
สิ่งที่น่าสนใจเกี่ยวกับทั้งหมดนี้คือวิธีที่สูตรกำลังสอง (∗) เกิดขึ้นจากปัญหาดังกล่าว. หลังจากนั้น, เราไม่ได้แก้สมการกำลังสองที่นี่, แต่เป็นสมการคู่กัน (1) และ (2).
หาดูได้ไม่ยาก, โดยใช้สัญกรณ์ของวันนี้. จาก (1) เราได้ y=s-x, ซึ่งเมื่อเปลี่ยนเป็น (2) ให้:
NS(NS−NS)=เอ.
NSNS−NS2=เอ.
NS2−NSNS+เอ=0.
ดังนั้น, (1) และ (2) เทียบเท่ากับการแก้สมการกำลังสอง x2-sx+a=0. โดยเฉพาะ, นี่บอกเราว่าในสมการกำลังสองนี้, สัมประสิทธิ์ของ x คือค่าลบของผลรวมของทั้งสองคำตอบ (สมการ (1) ), และสัมประสิทธิ์ของหนึ่งเป็นผลคูณของทั้งสองโซลูชั่น (สมการ (2) ).



ทิ้งคำตอบไว้
คุณต้อง เข้าสู่ระบบ หรือ ลงทะเบียน เพื่อเพิ่มคำตอบใหม่.